線対称と対頂角の利用
例題
下の図で、\(\angle APX=\angle BPY\) となるような点 \(P\) を、\(XY\) 上に作図しなさい。
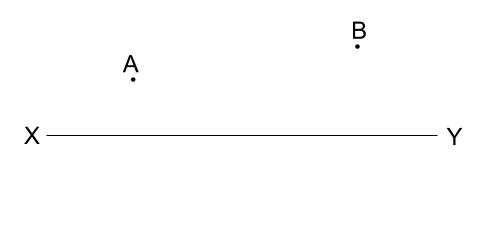
解説
作図方法がわからないとき、まずは完成形をラフスケッチします。
その完成形の図形的性質を探るのです。
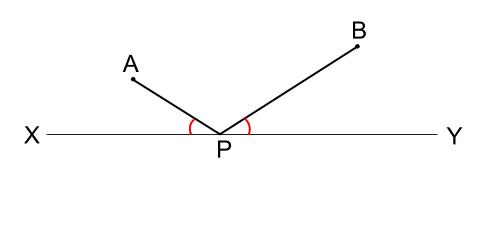
上図をみて、何か思いつくことはないでしょうか。
なかなか難しいですね。
直線 \(BP\) を延長してみましょう。
赤い角と青い角は対頂角で等しいので、赤い角とピンクの角が等しいならば、
青い角とピンクの角が等しいことになります。
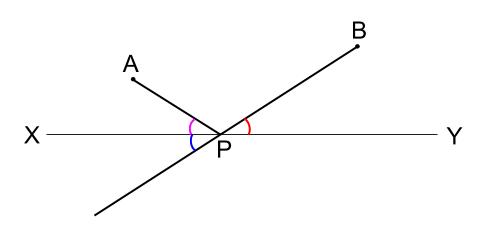
つまり、下図のピンクと青い直線が、\(XY\) を軸として線対称です。
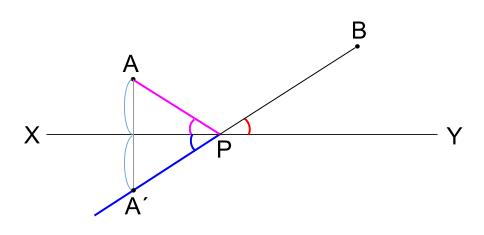
よって、\(A´\) を作図することができれば、点 \(P\) を作図できます。
※ところで、この点 \(P\) の位置は、\(AP+BP\) が最短となる点 \(P\) の位置と同じですね。
作図の方針がたちました。
1.点 \(A\) と対称な点 \(A´\) を、\(XY\) を対称の軸としてとる。
2.直線 \(A´B\) と 直線 \(XY\) の交点を 点 \(P\) とする。
作図
点 \(A\) を中心に円かき、直線 \(XY\) との交点をとる
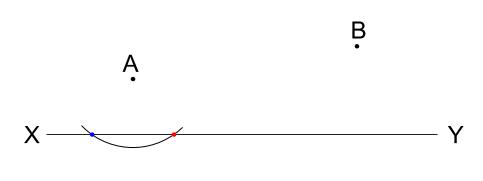
直線 \(XY\) との交点を中心に円を \(2\) つかく
交点が \(A´\)
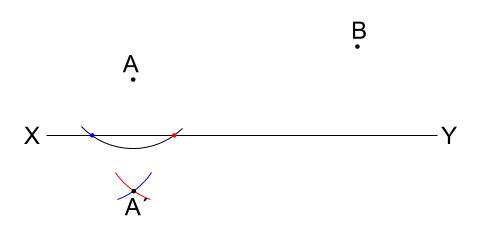
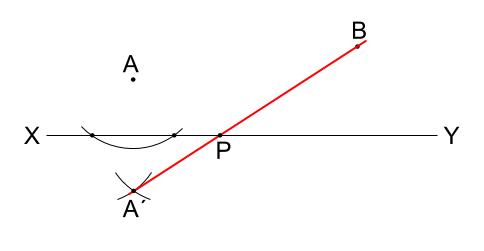
直線 \(A´B\) と直線 \(XY\) の交点が \(P\)
スポンサーリンク
