問題
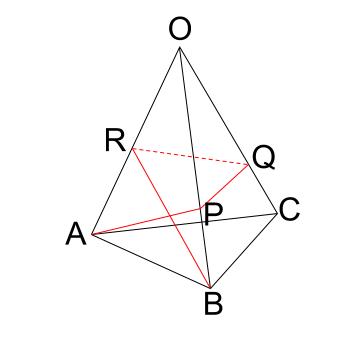
下図は、正三角形 \(ABC\) を底面とする三角錐で、側面の \(3\) つの三角形はすべて合同な二等辺三角形です。\(OA\) の長さは \(12cm\)、頂角 \(AOB\) の大きさは \(30°\) です 。辺 \(OB,OC,OA\) 上にそれぞれ点 \(P,Q,R\) をとって、 \(4\) つの直線の長さの和、\(AP+PQ+QR+RB\) が最短になるときを考えます。
(1)\(OP\) の長さと \(OQ\) の長さを求めなさい。
(2)この三角錐を、\(3\) 点 \(P,Q,R\) を通る平面で切断したとき、点 \(O\) を含む立体の体積は、もとの三角錐の体積の何倍か求めなさい。
解説
(1)も(2)も、重要な図形のテクニックが学習できる良難問です。
立体の表面を結ぶ線分を考えるとき、展開図をかいて考えます。
重要な解法テクニックであり、必ず暗記しておかねばなりません。
展開図をかくのですが、「展開図そのもの」をかくわけではありません。
直線が通る面のみを、平面で考えるのです。
三角形 \(OAB\) は \(2\) 回通過しますので、\(2\) つかきます。
底面は直線が通過しないため、かく必要はありません。
頂角が \(30°\) の二等辺三角形を \(4\) つ並べます。
\(30°,60°,90°,120°\) なので、正三角形や直角を意識してかきます。
正三角形をフリーハンドでサッとかく練習は、必ずしておきましょう。
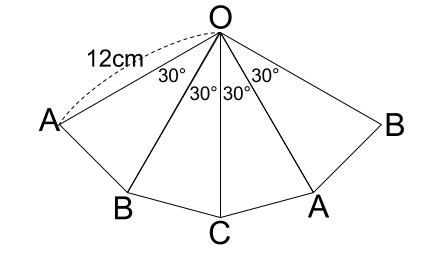
このような図は、一発できれいにかける必要はありません。
下書きして完成図をイメージしてから、改めてかくのです。
さて、\(4\) つの直線の長さの和、\(AP+PQ+QR+RB\) が最短になるのは、一直線のときです。
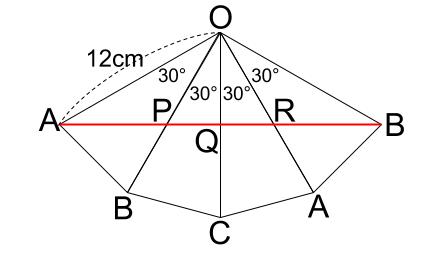
(1)\(OP\) の長さと \(OQ\) の長さ
さて、下図の青い三角形は、正三角形を半分にした、有名三角形です。三角定規型ですね。
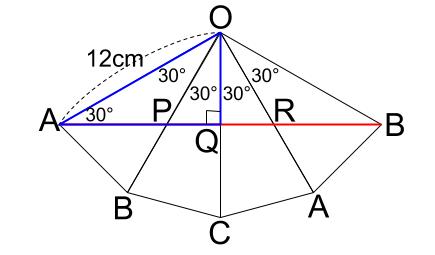
より、\(OQ=12×\displaystyle \frac{1}{2}=6\)
次に、三角形 \(OPQ\) に着目すると、こちらも角度から、正三角形を半分にした、有名三角形だとわかります。
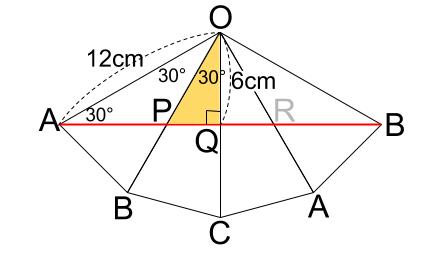
より、\(OP=6×\displaystyle \frac{2}{\sqrt{3}}=\displaystyle \frac{12}{\sqrt{3}}=4\sqrt{3}\)
以上求まりました。
(2)三角錐 \(O-PQR\) と三角錐 \(O-ABC\) の体積比
上で考察したことにより、\(OP=OR\) がわかります。
これをもとに、正しい見取り図をかくと下図のようになります。
※完璧に正しい見取り図ではありません。
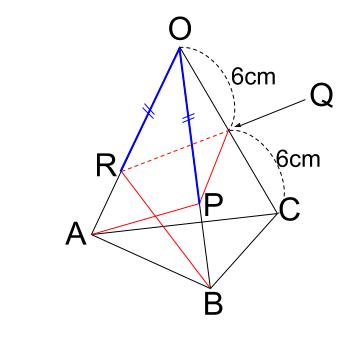
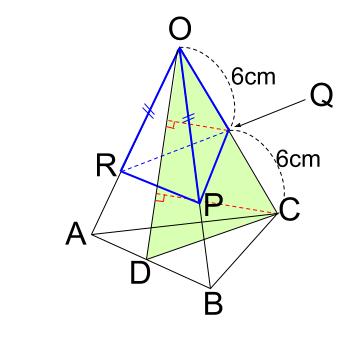
より、三角錐 \(O-PQR\) は下図です。

このとき、
三角錐 \(O-PQR\) の底面は、三角形\(ORP\)
三角錐 \(O-ABC\) の底面は、三角形\(OAB\)
と見ると、体積の比較が簡単になります。
三角形\(ORP\) と三角形\(OAB\) は、相似比のわかるピラミッド型相似なので、面積比がでます。
\(OR=OP=4\sqrt{3}\)、\(OA=12\) なので、
相似比は \(4\sqrt{3}:12=\sqrt{3}:3\)
より、面積比は
\((\sqrt{3})^2:3^2=3:9=1:3\)
高さの比は、下図の緑の三角形 \(ODC\) に着目して得られます。
\(D\) は \(AB\) の中点です。
緑の三角形 \(ODC\) をぬき出すと
\(OH_{1}Q\) と \(OH_{2}C\) はピラミッド型相似で、相似比は \(6:12=1:2\)
つまり、高さの比は \(1:2\) です。
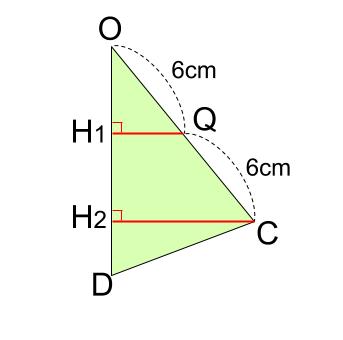
※図は不正確です。高さの比 \(1:2\) が理解できればそれでOKです。
よって、底面積比が \(1:3\) で、高さの比が \(1:2\) なので、体積の比は、
\(1×1:3×2=1:6\)
つまり、この切断によって得られる立体のうち、点 \(O\) を含む方は、もとの立体の体積の
\(\displaystyle \frac{1}{6}\) 倍です。
以上求まりました
スポンサーリンク
