正解率 \(0\) %
岐阜県の公立高校の入試問題・数学で出題された難問です。
正解率 \(0\) %だったそうです。
難問ですが、決して意地悪な出題ではありません。
たくさんの要素がつまった良問です。
得るものが多い一題ですので、ぜひ何度も読み返して身につけてください!
問題
下の図で、 \(4\) 点 \(A,B,C,D\) は円 \(O\) の周上にあり、 \(AC\) は \(O\) の直径で、\(AH\) は三角形 \(ABD\) の頂点 \(A\) から辺 \(BD\) にひいた垂線である。また、直径 \(AC\) と \(BD\) の交点を \(E\) とする。\(AC=10cm\)、\(CD=6cm\)、\(\angle EAH=\angle DAH\) のとき、\(BE\) の長さを求めなさい。
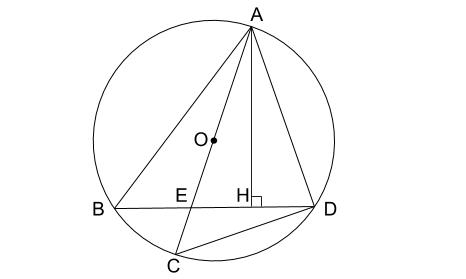
解説
\(AC=10cm\)、\(CD=6cm\) と図にかきこめば、自然と下の赤い三角形に目が行きますね。
\(AC\) が直径なので、円周角の定理より、\(\angle ADC=90°\)
三平方の定理より \(AD=8cm\)
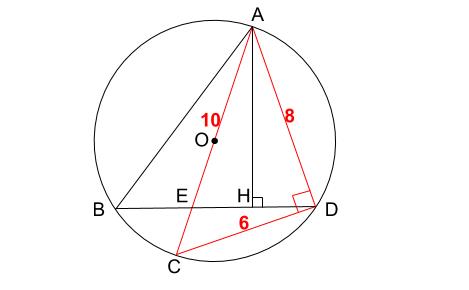
また、\(\angle EAH=\angle DAH\) より、三角形 \(AED\) は二等辺三角形なので、\(AE=8, EC=2\)
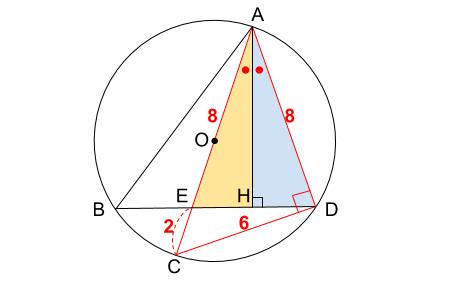
ここまでは迷わずこれますね。
次に見えるのは、円周角の定理より等しい大きさの角でしょう。
これも多くの類題と同タイプなので、すぐに反応できないといけません。
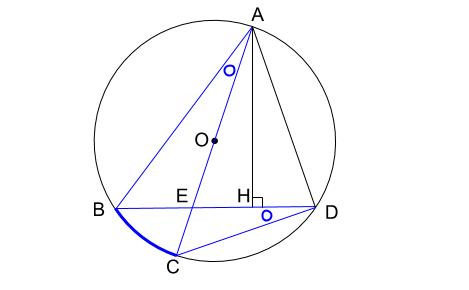
このことから、三角形 \(ABE\) と三角形 \(DCE\) が相似であることがわかります。
これは他の問題でも非常によく出る図形です。
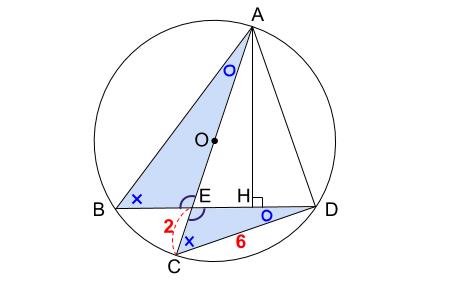
※\(\angle ABE=\angle DCE\) も、弧 \(AD\) の円周角より等しいですね。
ここまでは難しいことはありません。普通レベルです。
ここからが本番です。
さて、どうやって解き進めたら良いのでしょうか・・・
解法1・式処理で押す!
図形的性質に気づくことで、スルッと解けるのが理想ですが、思いつかないときには式処理でガツガツ進めます。文字でおいて、方程式をたてるのです。
とにかく求めたい長さ、\(BE=x\) とおいてみましょう。
すると、\(AB=3x\) です。
これは、三角形 \(ABE\) と三角形 \(DCE\) が相似であり、青バツ(×)の角を挟む \(2\) 辺の長さの比が \(1:3\) だからです。
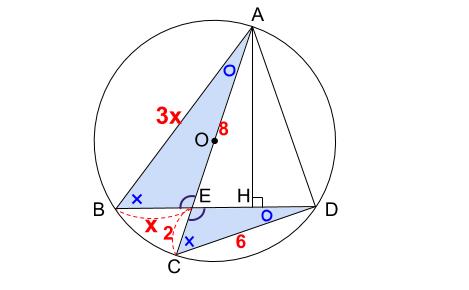
さて、三角形 \(ABE\) と三角形 \(DCE\) が相似で相似比が \(x:2\) なので、
\(EA:ED=x:2\)
より、\(ED=EA×\displaystyle \frac{2}{x}=8×\displaystyle \frac{2}{x}=\displaystyle \frac{16}{x}\)
よって、\(EH=\displaystyle \frac{16}{x}×\displaystyle \frac{1}{2}=\displaystyle \frac{8}{x}\)
あとは、三平方の定理で解決します。
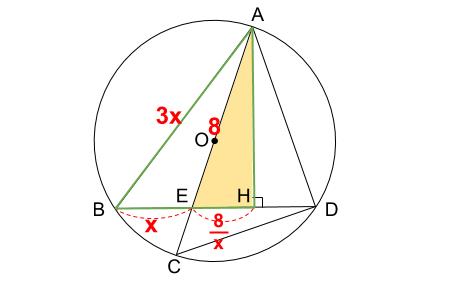
緑三角形 \(ABH\) より、
\(AH=(3x)^2-(x+\displaystyle \frac{8}{x})^2\)
クリーム色三角形 \(AEH\) より、
\(AH=8^2-(\displaystyle \frac{8}{x})^2\)
よって、
\((3x)^2-(x+\displaystyle \frac{8}{x})^2=8^2-(\displaystyle \frac{8}{x})^2\)
あとは、この式を計算していくのみです。
\(9x^2-(x^2+16+\displaystyle \frac{64}{x^2})=64-\displaystyle \frac{64}{x^2}\)
\(9x^2-x^2-16-\displaystyle \frac{64}{x^2}=64-\displaystyle \frac{64}{x^2}\)
\(8x^2-16=64\)
\(x^2=10\)
\(x=\pm \sqrt{10}\)
もちろん \(x\) は正なので、
\(x= \sqrt{10}\)
これで求まりました!!
解法2・もう1つの相似
次に紹介する解き方は、おそらく作問者が想定していたであろう解法です。
珍しい相似に気づかなくてはならないため、入試本番中の焦っている中では、なかなか厳しいことでしょう。
ずばり、
下の直角三角形 \(2\) つが相似です。
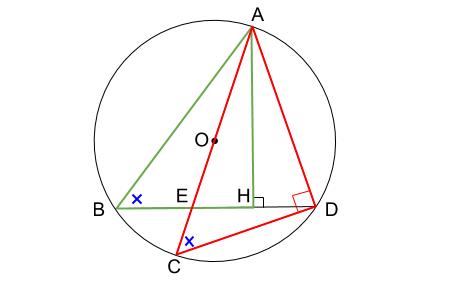
赤い直角三角形の辺の比は \(3:4:5\) なので、緑三角形 \(BHA\) の辺の比も \(3:4:5\) です。
より、\(AB:BH:HA=5:3:4\)
かつ、\(AB:BE=3:1\)・・・三角形 \(ABE\)と三角形 \(DCE\)が相似なので
より、\(AB=15x\) とすると、下図のようになります。
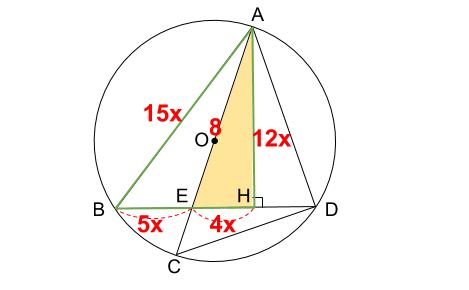
さて、クリーム色の直角三角形 \(AEH\) に三平方の定理を使うと、
\((4x)^2+(12x)^2=8^2\)
\(160x^2=64\)
\(x^2=\displaystyle \frac{2}{5}\)
\(x=\pm \sqrt{\displaystyle \frac{2}{5}}=\pm \displaystyle \frac{\sqrt{10}}{5}\)
もちろん \(x\) は正なので、
\(x= \displaystyle \frac{\sqrt{10}}{5}\)
\(BE=5x=\sqrt{10}\)
これで求まりました!!
解法3・角の2等分と辺の比
図形の性質をさぐっているとき、以下のことに気づいたでしょうか?
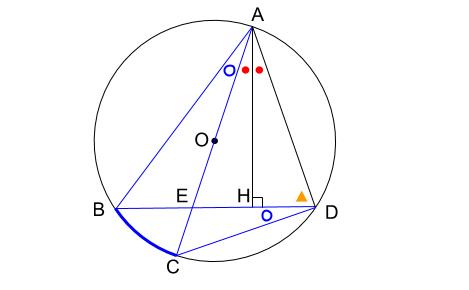
\(D\) の角に注目すれば、青丸とオレンジ三角の和は \(90°\)
三角形 \(AHD\) の内角に注目すれば、赤丸とオレンジ三角の和は \(90°\)
合わせて、青丸と赤丸は等しい
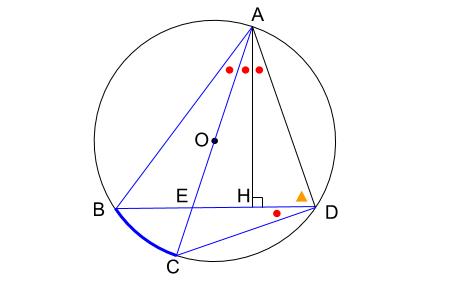
このことに気付いたのだけれど、まったく先に進めなかった・・・
という人もいることでしょう。
「角の2等分線と線分の比」についての知識があれば、力技で突破できます。
どこで役に立つかわかりません。
「角の2等分線と線分の比」を知らない人はおさえておきましょう。
三角形 \(ABH\) において \(AE\) が角 \(A\) の \(2\) 等分線なので、下図のように辺の長さをおけます。
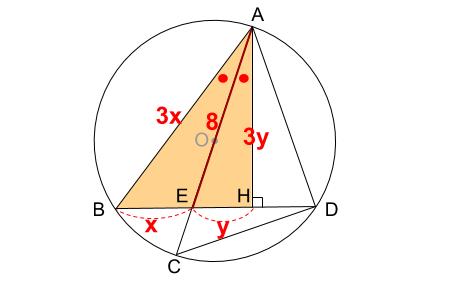
あとは、三平方の定理で解決します。
ここで、計算を簡単にするために、\(y=1\) のときの相似な三角形で長さを求めましょう。
三角形 \(AEH\) に三平方の定理を使うと、\(AE=\sqrt{10}\) なので、
これは、本来の図と相似比が \(8:\sqrt{10}\) です。
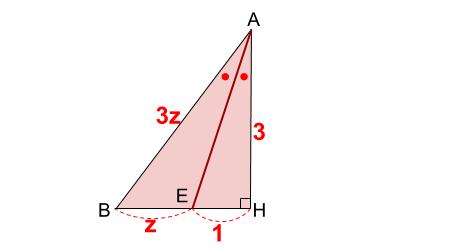
三角形 \(ABH\) に三平方の定理を使うと
\((3z)^2=(z+1)^2+(3)^2\)
あとはこの \(2\) 次方程式を解きます。
\(9z^2=z^2+2z+1+9\)
\(8z^2=2z+10\)
\(4z^2-z-5=0\)
\((4z-5)(z+1)=0\) と因数分解できるのですが、これは中学生には厳しいですね。
解の公式で解くと、
\(z=\displaystyle \frac{5}{4},-1\)
\(z\) は正なので、\(z=\displaystyle \frac{5}{4}\)
本来の図と相似比が \(8:\sqrt{10}\) の図で求めたので、本来の図での \(BE\) の長さは、
\(\displaystyle \frac{5}{4}×\displaystyle \frac{8}{\sqrt{10}}=\sqrt{10}\)
これで求まりました!!
スポンサーリンク
