立体の表面の最短距離
立体の表面を結ぶ線分を考えるとき、展開図をかいて考えます。
重要な解法テクニックであり、必ず暗記しておかねばなりません。
例題1
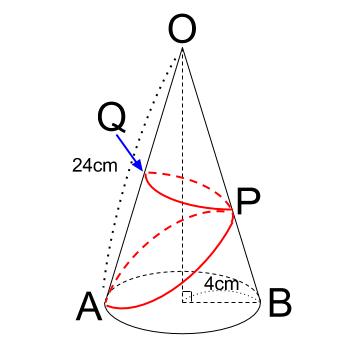
下の図のように、底面の半径が \(4cm\) で、母線の長さが \(24cm\) の円すいに、底面の点 \(A\) から側面を通って \(2\) 周糸をまきつけた。糸の長さが最も短くなるとき、 \(OB\) 上の点 \(P\) 、\(OA\) 上の点 \(Q\) を通った。\(AB\) は底面の円の直径である。
このとき、糸の長さを求めなさい。
また、\(OP,OQ\) の長さを求めなさい。
解答
糸が \(2\) 周とありますが、図からイメージできますか?
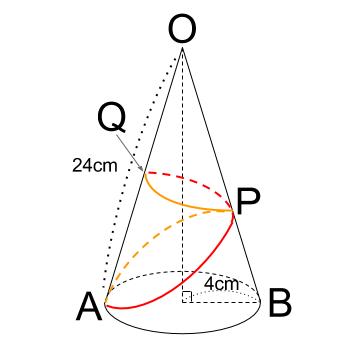
下図で説明すると、
赤色、\(A\) から \(P\) を通って \(Q\) までが \(1\) 周です。
オレンジ色、\(Q\) から \(P\) を通って \(A\) までで \(2\) 周です。
さて、円すいの展開図をかいて解きます。
展開図で考えるということは、暗記すべき解法知識ですね。
糸の通過している面のみをかけばよいので、
底面の円をかく必要はありません。側面のみをかきましょう。
そして、
側面は \(2\) つつなげてかきます。
赤の \(1\) 周目と、オレンジの \(2\) 周目は、別の側面に作図するのです。
とにかくやり方をみて理解・暗記してください!
側面はおうぎ形で、その中心角は
\(360×\displaystyle \frac{4}{24}=60°\)
より、中心角 \(60°\) のおうぎ形を \(2\) つ並べてかきます。
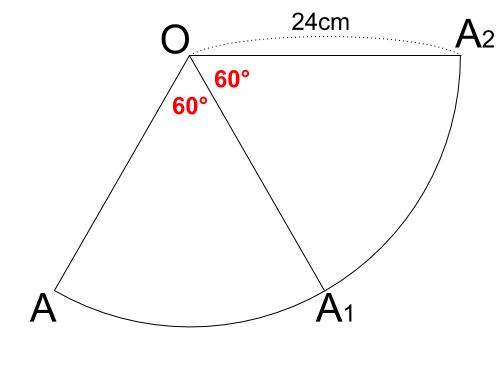
\(OA\) で切り開いた展開図を \(2\) つです。
組み立てたら一致する場所は同じ点です。
\(60°\)、\(120°\) の作図は、フリーハンドで練習しておきましょう。
厳密な作図である必要はありません。
正三角形をまず作図するのです。そこに弧をつけ足します。
糸の長さ
\(A\) から\(2\) 周後の \(A\) までを結ぶ最短距離は、一直線です。
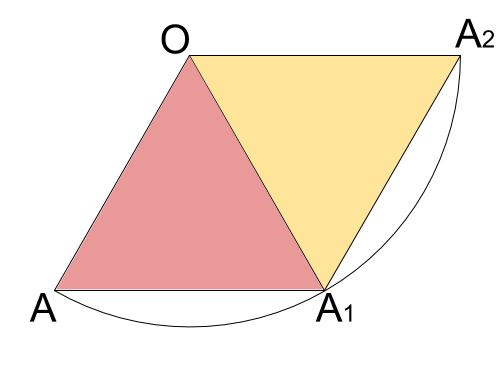
よって、まきつけた糸は下図のようになっています。
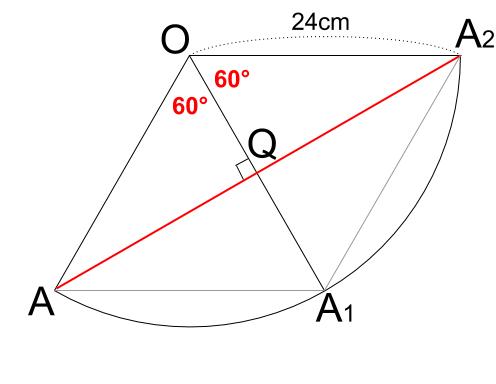
この図は \(OA_{1}\) を軸に左右対称であり、四角形 \(OAA_{1}A_{2}\) はひし形です。
ひし形の対角線は直交します。このような図形的考察から、\(AQ\) が正三角形 \(OAA_{1}\) の高さになっていることがわかります。
よって、 \(AQ=24×\displaystyle \frac{\sqrt{3}}{2}=12\sqrt{3}cm\)
まきつけた糸の長さは、\(AQ\) の \(2\) 倍なので、
\(12\sqrt{3}×2=24\sqrt{3}cm\)
求まりました。
\(OQ\) の長さ
\(OQ\) は \(OA_{1}\) の中点です。
上図から明らかですね。
よって、\(OQ=24×\displaystyle \frac{1}{2}=12cm\)
求まりました。
\(OP\) の長さ
母線 \(OB\) は、点 \(A\) と反対の位置にあります。
つまり、、点 \(A\) から底面の円をぐるり一周すると \(A\) にもどるのですが、そのちょうど半分の地点が点 \(B\) です。
つまり、中間地点なのです。
よって、 \(B,P\) は下図の位置にあります。
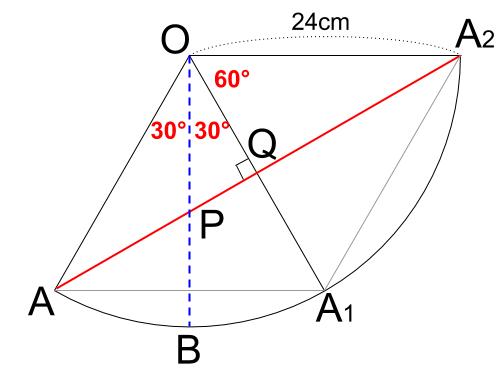
角度について考察すると、三角形 \(OPQ\) が、正三角形を半分にした直角三角形なので、
\(3\) 辺の辺の比は \(2:1:\sqrt{3}\) です。
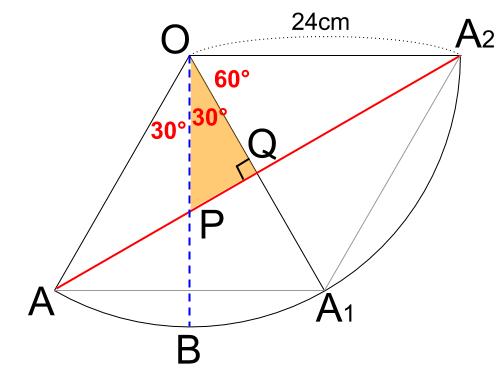
よって、
\(OP=OQ×\displaystyle \frac{2}{\sqrt{3}}=12×\displaystyle \frac{2}{\sqrt{3}}=8\sqrt{3}cm\)
以上、求まりました。
スポンサーリンク
