問題
Aさんは、1日練習して1日休み、Bさんは2日練習して1日休み、Cさんは3日練習して1日休みがある部に所属している。A、B、Cの3人とも1週目の月曜日から練習を始めると、練習日は下の表のようになる。ただし、○は練習日、×は休みの日を表している。3人は、3週目以降も同様の日程をくりかえします。
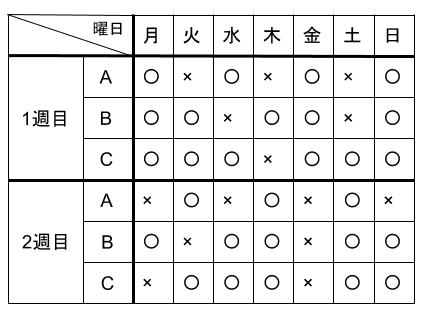
(1)A、B、Cの3人が同時に休みとなる初めての木曜日は、練習開始日から数えてア日目である。
(2)練習開始日から数えて100日目までに、A、B、Cの3人が同時に練習のある日の日数はイ日である。
解説
(1)3人が同時に休みとなる初めての木曜日
Aは2の倍数日目に休みとなる。
Bは3の倍数日目に休みとなる。
Cは4の倍数日目に休みとなる。
つまり、3人が同時に休みとなるのは、12の倍数日目である。
※2,3,4の最小公倍数は12
より、
12日目
24日目
36日目
のように、3人が同時に休みになる日が続いていく。
この中で、初めての木曜日を探せばよい。
曜日は、7ずつの周期であり、
木曜日は、4、11、18、・・・と続く。
※7でわると4余る数、あるいは、7の倍数+4
あとは探すだけである。
12は、7+5
24は、21+3
のように探せば、
60は、56+4
と見つかります。
よって、60日目です。ア=60です。
(2)100日目までに、3人が同時に練習のある日数
この問題では曜日は一切関係ありません。
3人の「練習」と「休み」の周期を合わせた周期は、12日周期。
より、この12日を1セットとして、全部かき出します。
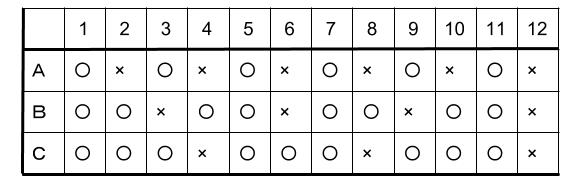
この1セットの中に、3人が同時に練習のある日数は4日あります。
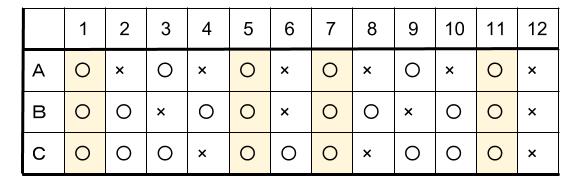
100÷12=8あまり4
なので、
12日1セットを8回繰り返したあと、さらにあと4日で100日目です。
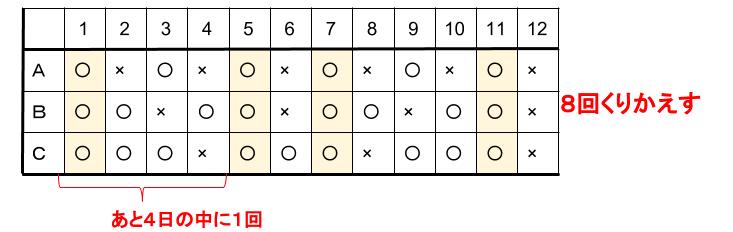
よって、4×8+1=33
33日です。
