問題
\(AB\) 上に点 \(D\) 、\(BC\) 上に点 \(E,F\) 、\(CA\) 上に点 \(G\)
があるような正方形 \(DEFG\) を、定規とコンパスを用いて作図しなさい。
解説
有名な作図です。
知らないと手も足も出ないタイプの問題です。
解説を読んで、理解・暗記をしましょう。
作図の方針は、相似の中心の利用です。
下図が作図の全容です。
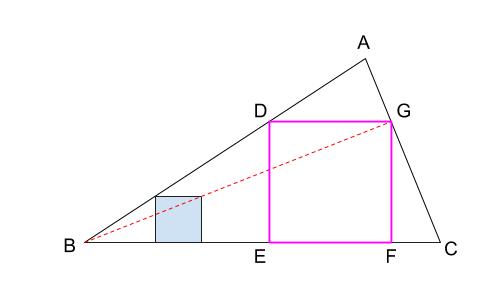
水色の小さい正方形と、赤い正方形 \(DEFG\) が相似です。
点 \(B\) が相似の中心となっています。
つまり、
水色の正方形を作図すれば、
点 \(G\) の位置が確定できるのです。
あとは、これを作図していくのみです。
まずは水色の正方形を作図します。
\(BP\) の長さはいくつでもかまいません。
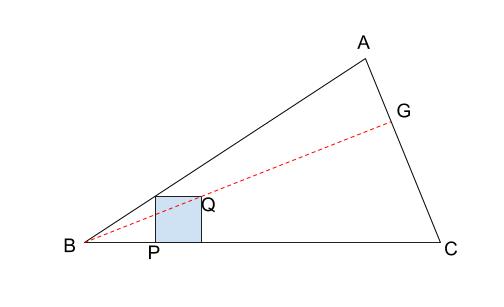
点 \(P\) を通る \(BC\) の垂線の作図からスタートです。
自動的に水色の正方形の大きさは決まります。
そして、\(BQ\) を結ぶ線分を延長して、点 \(G\) がとれます。
点 \(G\) から \(BC\) に垂線を引けば、その足が \(F\) ですね。
あとは、 \(GF\) の長さをコンパスでとって、
正方形 \(DEFG\) を作図します。

スポンサーリンク
