例題
\(1\) 辺が \(2cm\) の正四面体の体積を求めなさい。
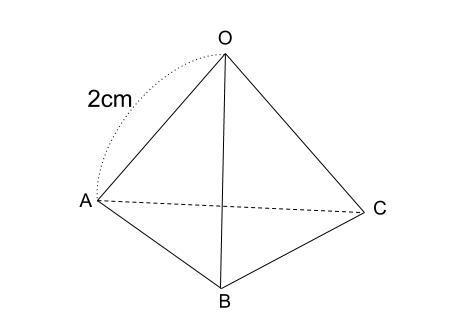
解説
この問題が、体積を答えさせるだけの問題として、
高校入試で出るとは考えにくいです。
なぜなら、\(1\) 辺が \(acm\) の正四面体の体積は \(\displaystyle \frac{\sqrt{2}}{12}a^3(cm^3)\)
という事実を暗記してきた生徒に対して無力な問題だからです。
しかし、
どのような過程を経て正四面体の体積を求めるのか、公式はどのように導かれるのか、
このような文章題が出題されることがあります。
中学数学における空間図形の知識をフル活用する良問です。
\(2\) つの代表的な解法を理解しておきましょう。
解法1 \(O\) から \(ABC\) へと垂線を下す。
正三角形の重心
正三角形 \(ABC\) を底面として、高さを求めます。
頂点 \(O\) から、底面 \(ABC\) に垂線を下します。
垂線と 底面 \(ABC\) の交わる点を \(H\) とします。
※「垂線の足」ともいいます。
\(H\) が、どのような位置にあるのか。
これについても、図形の有名知識です。
まずはこれについて考察しましょう。
正四面体を真上から見てみます。
当然、底面は正三角形です。
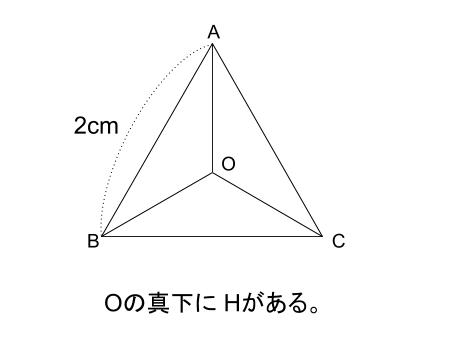
点 \(O\) の真下に 点 \(H\) があります。
正三角形の対称性から、\(AH\) の延長線上が \(BC\) の中点 \(M\) になります。
同様に、\(BH\) の延長線、\(CH\) の延長線は、向かいの辺の中点と交わります。
下図は底面の正三角形 \(ABC\) です。
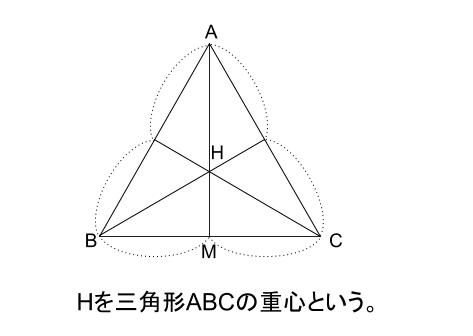
このような点 \(H\) の位置を、正三角形 \(ABC\) の重心といいます。
※重心は \(G\) を用いることが多いです。また、他の三角形の重心については、高校生になってから学習することになります。
重心の位置がどこなのか。
それを知るためには、\(AH:HM\) が必要です。
ずばり答えを書けば、
\(AH:HM=2:1\) です。
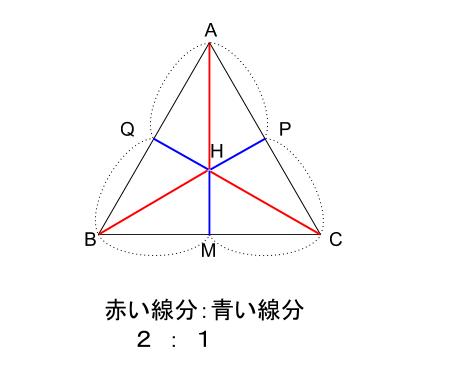
下の図において、
水色の三角形と、赤い三角形の面積の比を考えます。
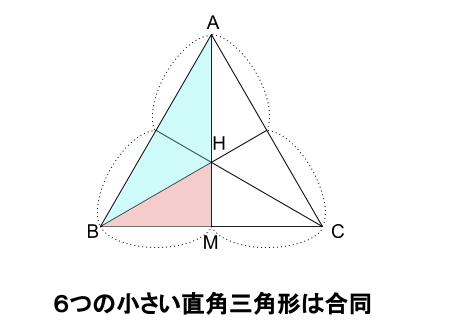
正三角形 \(ABC\) が \(6\) つの小さな直角三角形に割れましたが、
この \(6\) つはすべて合同です。
※簡単なので自分で考えてみてください。
水色の三角形は、小さな直角三角形が \(2\) つ分
赤色の三角形は、小さな直角三角形が \(1\) つ分
より、面積の比は \(2:1\) です。
これは、\(AH:HM\) の比と一致します。
\(AH\) と \(HM\) をそれぞれ底辺とすれば、
水色の三角形と、赤い三角形は高さが等しい三角形だからです。
もちろん正三角形の対称性より、
他の \(2\) つの線分も重心によって \(2:1\) に分かれます。
いよいよ体積
ようやく体積を求める準備が整いました。
この正四面体の高さ \(OH\) は下図のようになっています。
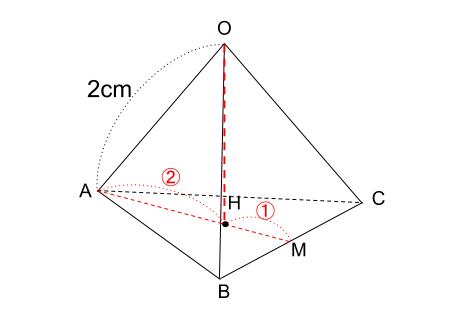
\(OH\) が何\(cm\) なのか求めます。
当然、三角形 \(OAH\) に三平方の定理を用います。
\(AM\) は \(1\) 辺が \(2cm\) の正三角形の高さなので、
\(AM=\sqrt{3}cm\) です。
より、 \(AH=\sqrt{3}×\displaystyle \frac{2}{3}=\displaystyle \frac{2\sqrt{3}}{3}\)
三角形 \(OAH\) に三平方の定理を用いて、
\(OH^2+(\displaystyle \frac{2\sqrt{3}}{3})^2=2^2\)
\(OH\) は \(0\) より大なので、
\(OH=\displaystyle \frac{2\sqrt{6}}{3}(cm)\)
です。
以上より、
底面積は、\(1\) 辺が \(2cm\) の正三角形の面積なので
\(2×\sqrt{3}×\displaystyle \frac{1}{2}=\sqrt{3}(cm^2)\)
高さは、\(OH=\displaystyle \frac{2\sqrt{6}}{3}(cm)\) なので、
正三角錐の体積は、
底面積×高さ× \(\displaystyle \frac{1}{3}\) より、
\(\sqrt{3}×\displaystyle \frac{2\sqrt{6}}{3}×\displaystyle \frac{1}{3}=\displaystyle \frac{2\sqrt{2}}{3}(cm^3)\)
と求まります。
解法2 正四面体を2つに割る
もう \(1\) つの解法は自力では思いつかないでしょうが、
有名なものです。
下図のように、 \(OA\) の中点 \(P\) をとり、正四面体を
三角形 \(PBC\) を底面とする三角錐 \(2\) つに分けます。
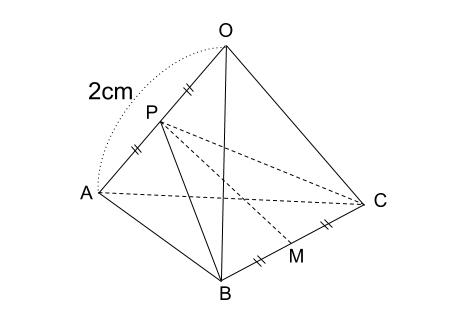
面 \(PBC\) と辺 \(OA\) が垂直であることはわかりますか?
そんな気もするけど、確信は持てない・・・
という人が大多数というところでしょう。
\(OA \perp PB\)
\(OA \perp PC\)
なので、面 \(PBC\) と辺 \(OA\) が垂直であるといえます。
ある平面 \(S\) と平面 \(S\) 上にない 直線 \(L\) の垂直を言うためには、
平面 \(S\) 上の少なくとも \(2\) 本の直線が、 直線 \(L\) と垂直であることが必要です。
よって、三角形 \(PBC\) を底面とし、髙さが \(1cm\) の三角錐 \(2\) つの体積の和が、
正四面体の体積になるので、
三角形 \(PBC\) の面積を求めます。
\(PM\) の長さは、三角形 \(PBM\) に三平方の定理を用いて
\(PM^2+1^2=\sqrt{3}^2\)
\(PM\) は \(0\) より大きいので、
\(PM=\sqrt{2}\)
よって、
三角形 \(PBC\) の面積は
\(2×\sqrt{2}×\displaystyle \frac{1}{2}=\sqrt{2}(cm^2)\)
よって、正四面体の体積は、
\(\sqrt{2}×1×\displaystyle \frac{1}{3}×2=\displaystyle \frac{2\sqrt{2}}{3}(cm^3)\)
と求まります。
立方体の中に正四面体
さらにもう \(1\) つ。
もっとも簡単に求める方法です。
ここでは、公式の導出をしてみましょう。
「正四面体は、立方体の内部にある」という、知らないとどうにもならない方法です。
下の図のように、立方体の頂点を結べば、
内部に正四面体があります。
すべての辺が正方形の対角線で等しく、すべての面が正三角形であることを
確認してください。
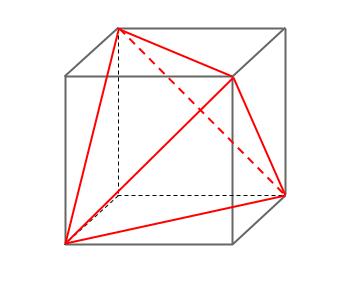
つまり、
立方体から、三角錐を \(4\) つ切り落とせば正四面体になります。
下の図の青い三角錐です。
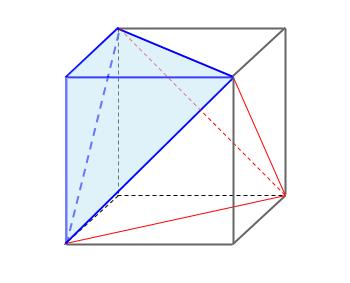
正方形の対角線の長さを \(a(cm)\) とします。
すると立方体の \(1\) 辺の長さは \(\displaystyle \frac{a}{\sqrt{2}}(cm)\) です。
立方体の体積は \((\displaystyle \frac{a}{\sqrt{2}})^3=\displaystyle \frac{\sqrt{2}}{4}a^3(cm^3)\)
三角錐 \(1\) つの体積は、立方体の体積の \(\displaystyle \frac{1}{6}\) なので、
※底面積が \(\displaystyle \frac{1}{2}\) 倍、高さは \(1\) 倍、錐体なので \(\displaystyle \frac{1}{3}\) 倍より。
よって、正四面体の体積は、立方体の \(1-\displaystyle \frac{1}{6}×4=\displaystyle \frac{1}{3}\)
以上から正四面体の体積は
\(\displaystyle \frac{\sqrt{2}}{4}a^3×\displaystyle \frac{1}{3}=\displaystyle \frac{\sqrt{2}}{12}a^3(cm^3)\)
と求まります。
スポンサーリンク
