正四角錐の良問・その２

問題

下の図のような、 $1$ 辺の長さが $2\sqrt{3}cm$ の正三角形 $ABC$ を底面とし、他の辺の長さが $4cm$ の正三角錐がある。辺 $BC$ の中点を $M$ とし、辺 $OC$ 上に線分 $AN$ と線分 $NB$ の長さの和が最も小さくなるように点 $N$ をとる。このとき、次の問いに答えなさい。

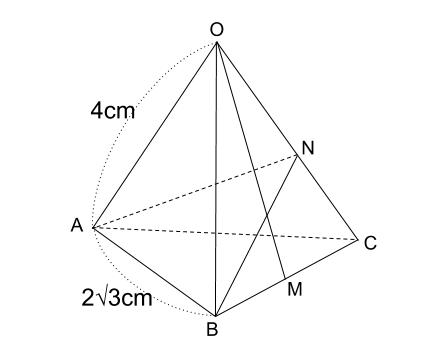
（１）この正三角錐の体積を求めなさい。
（２）線分 $ON$ と線分 $NC$ の長さの比を求めなさい。
（３）面 $OAB$ と点 $N$ との距離を求めなさい。

解説

やや難しいですが、とても学習効果の高い良問です。
中学数学の空間図形の応用のエッセンスがたくさん詰まっています。
内容が濃いため、解説は $2$ ページに分けます。

その１で、（１）（２）を求めました。
このページ、その２で、（３）を解説します。

その１・（１）（２）の解説

(1) 体積は $6cm^3$
(2) $ON:NC=5:3$ です。

（３）面 $OAB$ と点 $N$ との距離を求めなさい。

図示して考えるに決まっています。
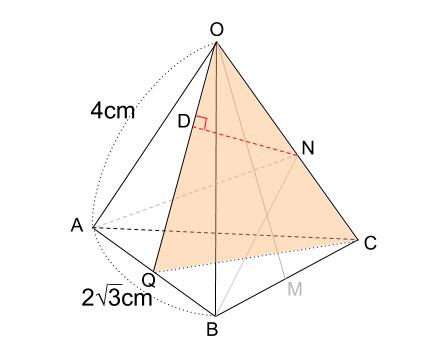
点 $N$ から面 $OAB$ へ垂線を下します。
この垂線の長さが聞かれていることです。
垂線の足を $D$ とします。
$ND$ の長さが求める長さ、最終目標です。

空間図形において、注目しているものを含む平面で考える。
これも必須知識です。
今回は、下図のような三角形 $OQC$ に着目します。
$Q$ はもちろん $AB$ の中点です。

何か思いつきますか？

とりあえず、（２）で点 $N$ の位置を求めたわけですから、
この結果を使うに決まっています。
数学では、前の小問の結果を利用して次を解くということが
よくありますので、これも意識しておきましょう。

つまり、$ON:NC=5:3$ とは、
下の図のように、$CE$ から $ND$ を求めろ、ということです。
三角形 $OEC$ と三角形 $ODN$ がピラミッド型の相似になっています。

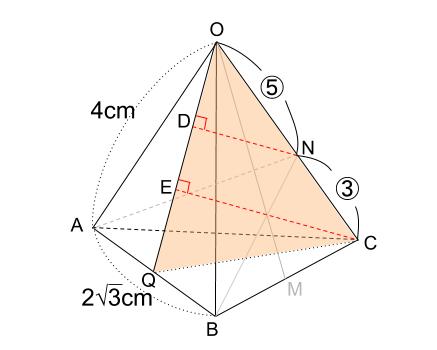
つまり、 $CE$ の長さを求めて、$\displaystyle \frac{5}{5+3}=\displaystyle \frac{5}{8}$ 倍すれば $ND$ が求まります。

では $CE$ はどうやって求めるのか。
代表的な $2$ つの解き方を確認しておきましょう。

体積の利用

$CE$ の長さは、底面を三角形 $OAB$ と見たときの
三角錐の髙さになっています。
つまり「体積」から計算できます。

その１で、「（１）この正三角錐の体積を求めなさい。」
を解説しております。
体積は $6cm^3$ です。

底面が $OAB$
高さを $CE$
その体積は $6cm^3$
これで $CE$ が計算できます。

$OAB$ の面積から求めましょう。
$OQ$ の長さは、三角形 $OAQ$ に三平方の定理を使うだけです。
$OQ^2+\sqrt{3}^2=4^2$
より $\sqrt{13}cm$ です。
よって、$OAB$ の面積は

$2\sqrt{3}×\sqrt{13}×\displaystyle \frac{1}{2}=\sqrt{39}(cm^2)$

つまり、三角錐の体積は
底面積×高さ÷３＝体積なので、

$\sqrt{39}×CE×\displaystyle \frac{1}{3}=6$

$CE=\displaystyle \frac{6\sqrt{39}}{13}$

$ND$ は $EC$ の $\displaystyle \frac{5}{8}$ 倍なので

$ND=\displaystyle \frac{6\sqrt{39}}{13}×\displaystyle \frac{5}{8}$

$ND=\displaystyle \frac{15\sqrt{39}}{52}$

これが求める長さです。

三平方の定理の利用

もう $1$ つ重要な必須の解法を紹介します。

先の図において
三角形 $OQC$ をぬき出します。

三角形 $OEC$ と三角形 $QEC$ に三平方の定理を用いれば
求まる形になっています。
$QE=x(cm)$ とおきます。

$OQ$ の長さは、上の解法でも求めましたが $\sqrt{13}cm$ です。

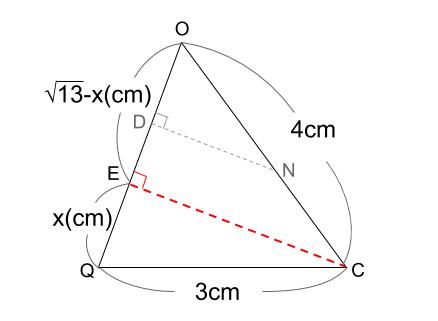
三角形 $OEC$ より
$EC^2=4^2-(\sqrt{13}-x)^2$・・・①

三角形 $QEC$ より
$EC^2=3^2-x^2$・・・②

①、②の右辺はどちらも $EC^2$ と等しいので

$4^2-(\sqrt{13}-x)^2=3^2-x^2$
これを整理します。
$16-(13-2\sqrt{13}x+x^2)=9-x^2$
$16-13+2\sqrt{13}x-x^2=9-x^2$
$3+2\sqrt{13}x=9$
$2\sqrt{13}x=6$
$\sqrt{13}x=3$

$x=\displaystyle \frac{3}{\sqrt{13}}$

$x=\displaystyle \frac{3\sqrt{13}}{13}$

これを、②に代入して $EC$ が求まります。

$EC^2=3^2-\displaystyle (\frac{3\sqrt{13}}{13})^2$

$EC^2=\displaystyle \frac{108}{13}$

$EC$ は $0$ より大なので、

$EC=\sqrt{\displaystyle \frac{108}{13}}$

$EC=\displaystyle \frac{\sqrt{108}}{\sqrt{13}}$

$EC=\displaystyle \frac{6\sqrt{3}}{\sqrt{13}}$

$EC=\displaystyle \frac{6\sqrt{3}×\sqrt{13}}{13}$

$EC=\displaystyle \frac{6\sqrt{39}}{13}$

長かった旅もようやく終わりです。

$ND$ は $EC$ の $\displaystyle \frac{5}{8}$ 倍なので

$ND=\displaystyle \frac{6\sqrt{39}}{13}×\displaystyle \frac{5}{8}$

$ND=\displaystyle \frac{15\sqrt{39}}{52}$

これが求める長さです。

スポンサーリンク