問題
下の図のような、 \(1\) 辺の長さが \(2\sqrt{3}cm\) の正三角形 \(ABC\) を底面とし、他の辺の長さが \(4cm\) の正三角錐がある。辺 \(BC\) の中点を \(M\) とし、辺 \(OC\) 上に線分 \(AN\) と線分 \(NB\) の長さの和が最も小さくなるように点 \(N\) をとる。このとき、次の問いに答えなさい。
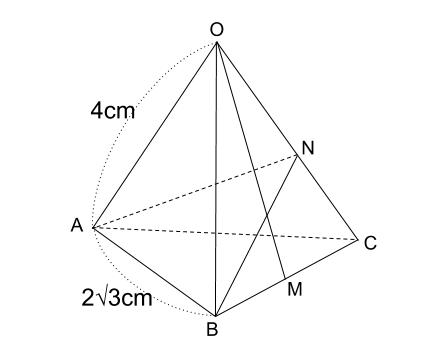
(1)この正三角錐の体積を求めなさい。
(2)線分 \(ON\) と線分 \(NC\) の長さの比を求めなさい。
(3)面 \(OAB\) と点 \(N\) との距離を求めなさい。
解説
やや難しいですが、とても学習効果の高い良問です。
中学数学の空間図形の応用のエッセンスがたくさん詰まっています。
内容が濃いため、解説は \(2\) ページに分けます。
その1では、(1)(2)まで
その2で、(3)を解説します。
(1)正三角錐の体積
正三角形の重心
正三角形 \(ABC\) を底面として、高さを求めます。
頂点 \(O\) から、底面 \(ABC\) に垂線を下します。
垂線と 底面 \(ABC\) の交わる点を \(H\) とします。
※「垂線の足」ともいいます。
\(H\) が、どのような位置にあるのか。
これについても、図形の有名知識です。
正三角形の重心です。
正三角形の重心を知らない人は、正四面体の体積と正三角形の重心
というページで、くわしく説明していますので、
まずはそちらを読んでください。
いよいよ体積
この正三角錐の高さ \(OH\) は下図のようになっています。
\(AM\) を \(2:1\) に分ける位置に点 \(H\) があります。
\(AM\) は\(1\) 辺が \(2\sqrt{3}cm\) の正三角形の高さで、 \(3cm\) です。
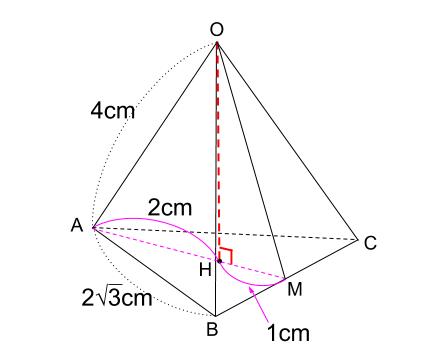
\(OH\) が何\(cm\) なのか求めます。
当然、三角形 \(OAH\) に三平方の定理を用います。
\(OH^2+2^2=4^2\)
\(OH\) は \(0\) より大なので、
\(OH=2\sqrt{3}(cm)\)
です。
ちなみに、三角形 \(OAH\) は辺の比から、\(30°,60,90°\) の
三角定規型になっています。
以上より、
底面積は、\(1\) 辺が \(2\sqrt{3}cm\) の正三角形の面積なので
\(2\sqrt{3}×3×\displaystyle \frac{1}{2}=3\sqrt{3}(cm^2)\)
高さは、\(OH=2\sqrt{3}(cm)\) なので、
正三角錐の体積は、
底面積×高さ× \(\displaystyle \frac{1}{3}\) より、
\(3\sqrt{3}×2\sqrt{3}×\displaystyle \frac{1}{3}=6(cm^3)\)
と求まります。
(2)線分 \(ON\) と線分 \(NC\) の長さの比
(2 )は(1)の体積とはまったく関係のない話題です。
「立体の表面上の線分の問題は、展開図で考える」という
必須の知識問題です。
展開図はすべてかく必要はありません。
\(AN\) と \(NB\) がある面だけでOKです。
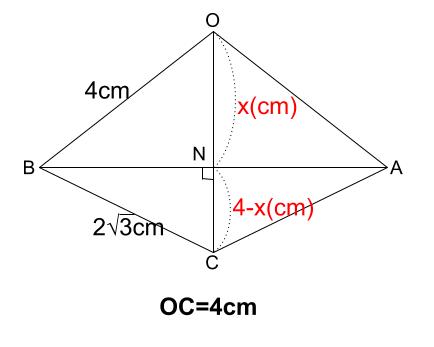
ここで、\(ON=x\) として、\(2\) 種類の三角形に三平方の定理を
使用します。
三角形 \(OBN\) より
\(BN^2=4^2-x^2\)・・・①
三角形 \(CBN\) より
\(BN^2=(2\sqrt{3})^2-(4-x)^2\)・・・②
①、②から \(BN^2\) を消します。
どちらの右辺も \(BN^2\) と等しいので、
\(4^2-x^2=(2\sqrt{3})^2-(4-x)^2\)
あとは計算するだけです。
\(16-x^2=12-(x^2-8x+16)\)
\(16-x^2=12-x^2+8x-16\)
\(16=+8x-4\)
\(20=8x\)
\(x=2.5\)
よって
\(ON=2.5(cm)\)
\(NC=1.5(cm)\)
なので、求める長さの比は
\(2.5:1.5=5:3\)
です。
スポンサーリンク
