問題
下の図は \(A,B,C,D,E,F\) を頂点とし、 \(3\) つの側面がそれぞれ長方形である三角柱で、 \(AD=5cm,DE=6cm,EF=4cm,\angle ABC=90°\) である。辺 \(AB\) 上に点 \(P\) を \(2\) つの線分 \(DP,PC\) の長さの和が最小となるようにとる。また、点 \(Q\) は、線分 \(AE\) と線分 \(DP\) との交点である。このとき、次の問いに答えなさい。
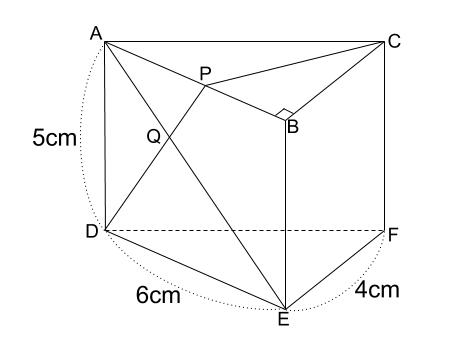
(1)辺 \(AC\) の長さを求めさない。
(2)線分 \(PB\) の長さを求めさない。
(3)線分 \(AQ\) と線分 \(QE\) の長さの比、\(AQ:QE\) を求めさない。
(4)四角形 \(ADFC\) を底面とする四角すい \(QADFC\) の体積を求めさない。
解説
(1)から(3)までは基本です。
一気に解説します。
(4)がこの問題のメインです。難問ですが、空間図形の力を養うための良問です。
(1)辺 \(AC\) の長さ
(1)は三角形 \(ABC\) に三平方の定理を使うだけ、 \(AC=2\sqrt{13}cm\) です。
(2)線分 \(PB\) の長さ
点 \(P\) の位置は、立体の表面上の最短距離から決まります。
このタイプの問題は「展開図」で解くという有名知識です。
展開図上で直線が最短です。
線分 \(DP,PC\) がある面のみでOKです。
下のピンクの「砂時計型相似」から求まります。
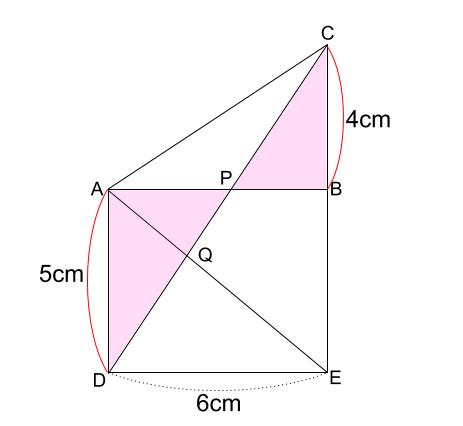
相似比は \(5:4\) なので、\(AP:PB=5:4\)
より、
\(6×\displaystyle \frac{4}{5+4}=\displaystyle \frac{8}{3}(cm)\)
これが求める線分 \(PB\) の長さです。
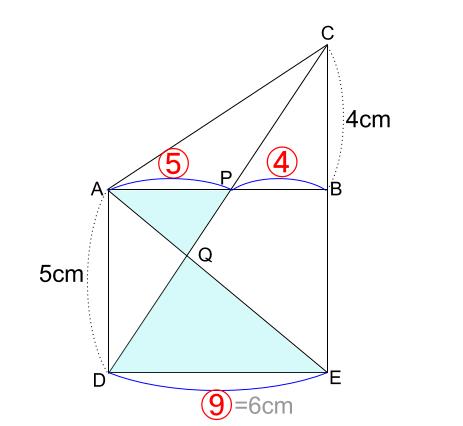
(3)線分 \(AQ\) と線分 \(QE\) の長さの比
下の水色の「砂時計型相似」から求まります。
(2)で、\(AP:PB=5:4\) と求めたので、これを使いましょう。
下図のようになっていて、
相似比は \(AP:ED=5:9\) です。
\(AQ\) と \(QE\) も、この相似な三角形の対応する辺なので、
その比は、\(5:9\) です。
いよいよ(4)!!
いよいよ本題です。
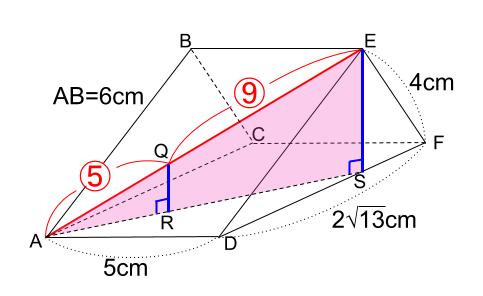
(4)四角すい \(QADFC\) の体積です。
点 \(Q\) がどのような位置にあるのか、(3)がヒントとなっています。
まずは問題の通り、
四角すい \(QADFC\) を、四角形 \(ADFC\) を底面とするような向きに置き直してみましょう。
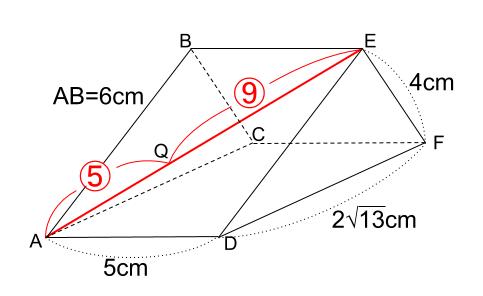
底面の 四角形 \(ADFC\) の面積は求められるので、
あとは高さがわかれば、四角すい \(QADFC\) の体積が求められます。
高さとは、下図のようになっていますね。
着目する線分を含む平面で考える、
これが空間図形を解くために必須の解法知識です。
三角形 \(AQR\) と三角形 \(AES\) がピラミッド型相似で、相似比が \(5:5+9=5:14\)
になっているので、
\(QR\) は \(ES\) の \(\displaystyle \frac{5}{14}\) 倍です。
\(2\) 通りの解き方
ここから先は、\(2\) 通りの解き方を示します。
具体的に \(QR\) の長さを求めるやり方。
もう \(1\) つは、体積比で求めるやり方。
どちらの解法もしっかりと理解して欲しい重要なものです。
具体的に \(QR\) の長さを求める
まずは、具体的に \(QR\) の長さを求めてみましょう。
\(QR\) は \(ES\) の \(\displaystyle \frac{5}{14}\) 倍なので、
\(ES\) の長さを求めます。
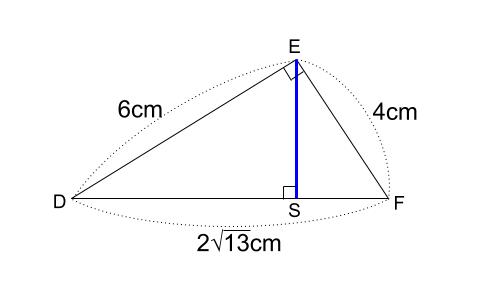
当然ですが、三角形 \(EDF\) に着目しましょう。
三平方の定理で \(ES\) の長さを求めるのは下手ですね。面倒です。
ここでは、「相似」か「面積」から求めましょう。
どちらの解き方も基本的な解法テクニックとして覚えていないといけません。
ここでは面積から求めましょう。
三角形 \(EDF\) の面積は、\(4×6×\displaystyle \frac{1}{2}=12\)
また、この三角形の面積は、底辺を \(DF\) 、高さを \(ES\) と見れば
\(2\sqrt{13}×ES×\displaystyle \frac{1}{2}=12\)
\(ES=\displaystyle \frac{12}{13}\sqrt{13}\)
よって、四角すい \(QADFC\) の体積は、
\(5×2\sqrt{13}×\displaystyle \frac{12}{13}\sqrt{13}×\displaystyle \frac{5}{14}×\displaystyle \frac{1}{3}=\displaystyle \frac{100}{7}\)
これが求める体積です。
比の活用で体積を求める
高さを具体的に求めなくとも、体積は出せます。
比の活用です。
解き方の大きな流れは上のものと変わりません。
\(ES\) の長さを出す直前までは同一です。
違いは、最後の計算処理のやり方です。
具体値ではなく比で処理しようという解法です。
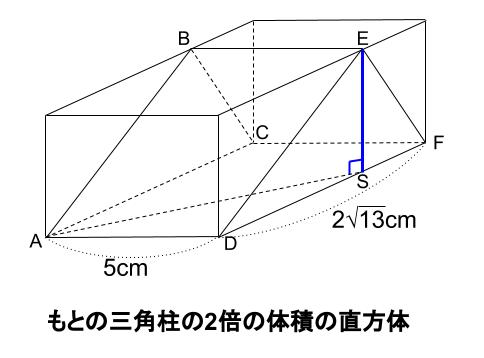
まず、はじめに与えられた三角柱の体積は、
底面を 三角形 \(DEF\) 、高さを \(AD=5cm\) と見れば簡単に求まります。
\(60cm^3\) です。
また、四角形 \(ADFC\) を底面、高さを \(ES\) とする四角柱(直方体)の体積は、
この三角柱の体積の \(2\) 倍で \(120cm^3\) です。
これを \(\displaystyle \frac{5}{14}\) 倍すれば、
四角形 \(ADFC\) を底面、高さを \(QR\) とする四角柱(直方体)の体積になります。
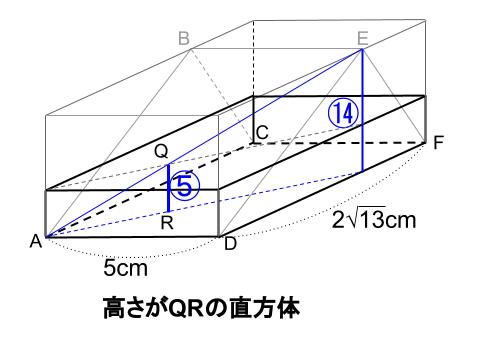
求める 四角すい \(QADFC\) の体積は、この直方体の体積の \(\displaystyle \frac{1}{3}\) 倍なので、
\(120×\displaystyle \frac{5}{14}×\displaystyle \frac{1}{3}=\displaystyle \frac{100}{7}\)
これで求まりました。
スポンサーリンク
