例題
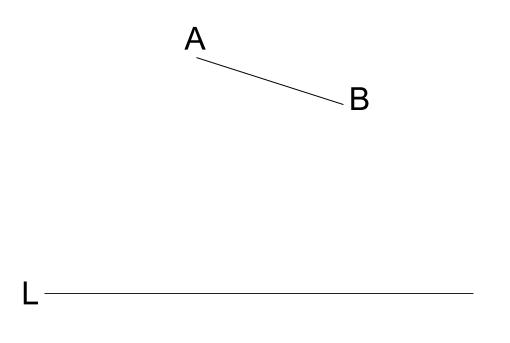
角 \(APB=30°\) となる点 \(P\) を、直線 \(L\) 上に作図せよ。
ただし、条件を満たす点 \(P\) の位置は \(2\) 箇所ある。片方を \(P_{1}\)、もう片方を \(P_{2}\) としなさい。
解説
難しいです。
こんなの自力で思いつけるとはとても思えません・・・
数学において、「様々な解法パターンを見ておく」
ということがどれほど重要か痛感されます。
さて、
どのように作図したら良いかわからないときは、
「完成図のラフスケッチ」です。
正しい\(P_{1}\)、\(P_{2}\) の位置はわからないので、だいたいでかきます。
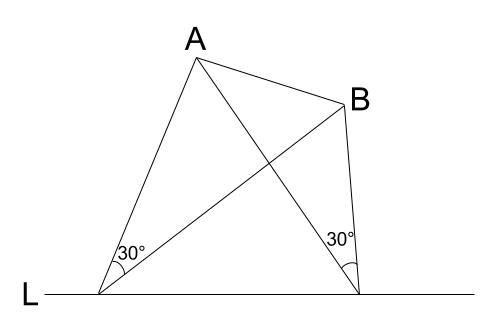
この図の図形的性質から、作図方法がわかるのですが・・・
ずばり、答えは「円周角の定理の逆」なのです。
つまり、
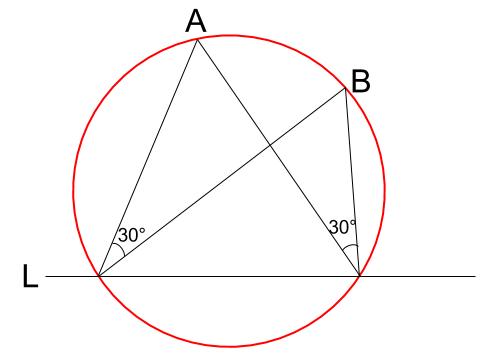
このような円が背景にあるということです。
これを自力で思いつかなくてもOKですよ。こういう解法もありなんだな!
と覚えてもらって、いつか類題を見たときにピンとくるようになりましょう。
で、あの円を作図するということは、あの円の中心と半径を定めるということですが・・・
ここから先は自力で思いついて欲しいです。
ずばり、
円周角ときたら、対になるもの、中心角です。
円周角が \(30°\) なのですから、中心角は \(60°\) です。
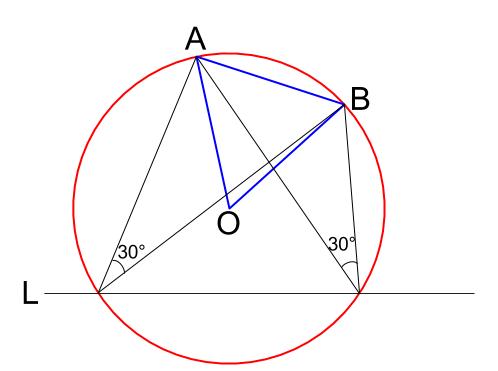
これって・・・正三角形の作図です!
以上、作図方法が見えましたね。
あとは手順にしたがって作図を進めていくのみです。
1.\(AB\) を \(1\) 辺とする正三角形を作図します。 \(A,B\) 以外の頂点を \(O\) とします。
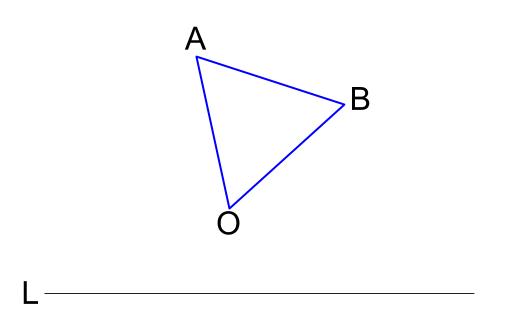
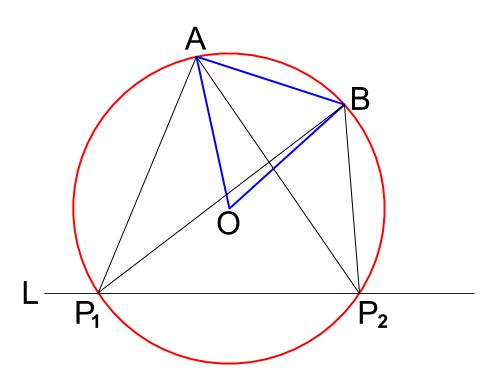
2. \(O\) を中心に、\(OA\) を半径とする円をかく。
直線 \(L\) との交点が \(P_{1}\)、\(P_{2}\) です。
作図完了です。
スポンサーリンク
