問題
\(AB=6cm,BC=10cm\) の長方形 \(ABCD\) があります。
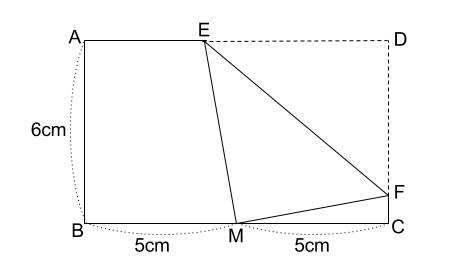
この長方形を、下の図のように、 \(D\) が \(BC\) の中点 \(M\) と
重なるように折ります。このとき、 \(CF\) の長さを求めなさい
解説
初見ではなかなか戸惑う問題でしょうか。
やはり、様々なパターンに慣れておくことが重要です。
中学数学においては、
未知のものを \(x\) などの文字でおき、
式をたてるのが鉄則です。
\(CF=x\) としてみましょう。
自動的に \(DF=6-x\) です。
そして、折り返しですから
\(MF=DF=6-x\) となります。
折り返す前の図を想定することも定番パターンです。
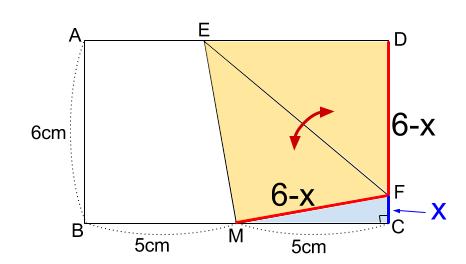
これで解決ですね。
もちろん
三平方の定理です。
右下の水色の直角三角形 \(FMC\) に三平方の定理を使います。
\((6-x)^2=5^2+x^2\)
あとはこの方程式を解くだけです。
\(36-12x+x^2=25+x^2\)
\(11=12x\)
\(x=\displaystyle \frac{11}{12}\)
これで求まりました。
別解
直角が、直線上にのっているので
直角三角形の相似の有名な配置です。
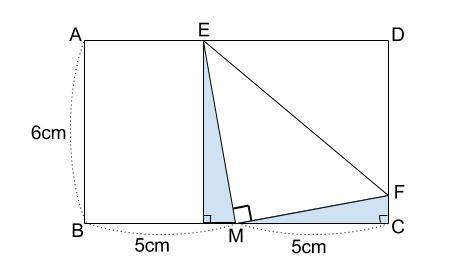
下図の水色の直角三角形が相似です。
※角度からわかります。
\(AB:MC=6:5\) より、
相似比は \(6:5\) です。
\(FC=5x\) とすると、下の図のように各長さが \(x\) を用いて表せます。
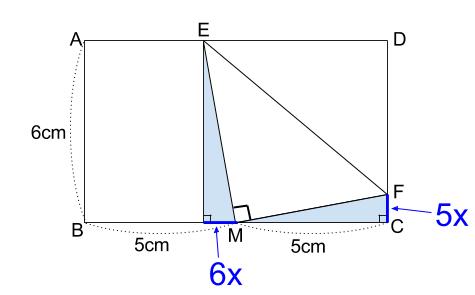
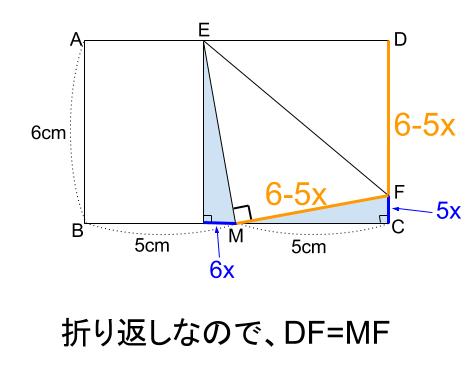
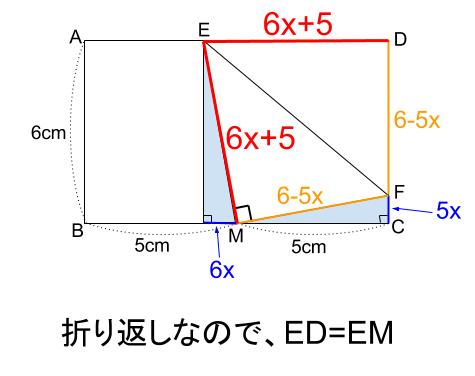
ここで改めて、水色の相似な直角三角形に着目します。
相似比は \(6:5\) だったので、
斜辺の長さの比は \(6:5\) です。
よって、
\(6x+5:6-5x=6:5\)
内項の積と外項の積は等しいので、
\(6(6-5x)=5(6x+5)\)
これを解いて、
\(x=\displaystyle \frac{11}{60}\)
求める長さは \(5x\) なので、
\(5x=\displaystyle \frac{11}{12}\)
スポンサーリンク
