問題
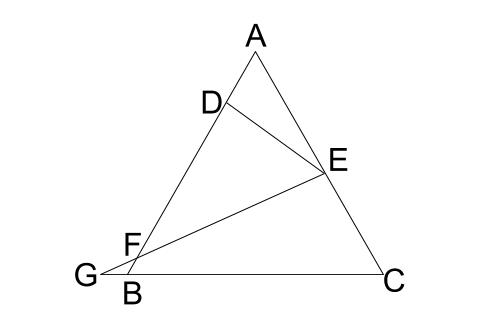
正三角形 \(ABC\) は \(1\) 辺の長さは \(14cm\) で、\(AD=3cm,AE=8cm\) 、角 \(DEF=60°\) です。
以下のものを求めなさい。
(1)\(BG\) の長さ
(2)三角形 \(DEF\) の面積
(3)\(DE\) の長さ
解説
(1)\(BG\) の長さ
三角形 \(ADE\) と三角形 \(CEG\) が相似です。角度を考察することでわかります。
\(AD\) と \(CE\) が対応する辺なので、相似比は \(3:6=1:2\)
より、\(EA×2=GC\)
\(GC=8×2=16\)
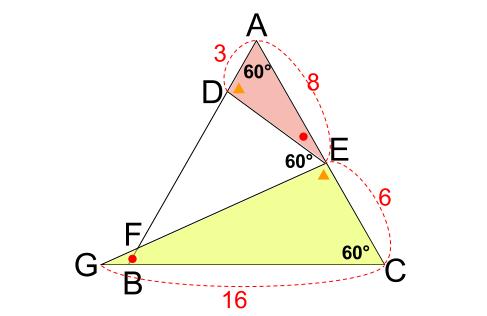
よって、\(BG=GC-BC=16-14=2\)
以上求まりました。
(2)三角形 \(DEF\) の面積
\(AH=8cm\) となるように点 \(H\) をとると \(HE /\!/ GB\) なので、砂時計型相似ができます。緑と黄色の三角形です。
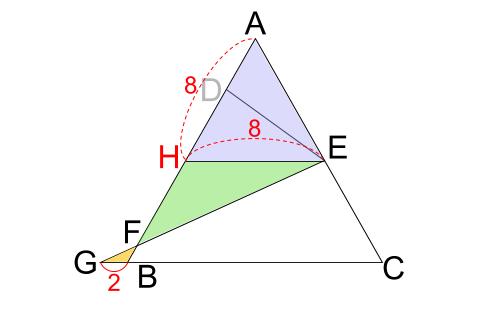
相似比は \(HE:BG=8:2=4:1\)
\(FH\) と \(FB\) も対応する辺で、その長さの比は \(4:1\) なので、
より、\(FH=HB×\displaystyle \frac{4}{4+1}=6×\displaystyle \frac{4}{5}=4.8\)
三角形 \(DEF\) の面積は、\(DF\) を底辺、点 \(E\) を頂点と見ることで求められます。
三角形 \(DEF\) は正三角形 \(AHE\) と高さの等しい三角形です。
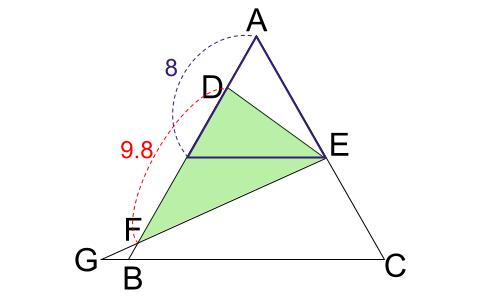
底辺の比は、\(9.8:8\) なので、
三角形 \(DEF\) の面積は、正三角形 \(AHE\) の面積\(×\displaystyle \frac{9.8}{8}\) となります。
よって、\(8×8×\displaystyle \frac{\sqrt{3}}{2}×\displaystyle \frac{1}{2}×\displaystyle \frac{9.8}{8}=\displaystyle \frac{98\sqrt{3}}{5}\)
以上求まりました!
別解1
下図のように、\(EI\) を引くことで、ピラミッド型相似から \(FB=1.2\) を求めて、
\(DF=9.8\) を得ることもできます。
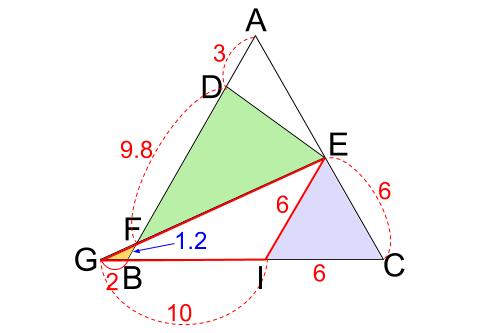
別解2
\(DF=9.8\) の後、内部底辺の利用で面積を求めることもできます。
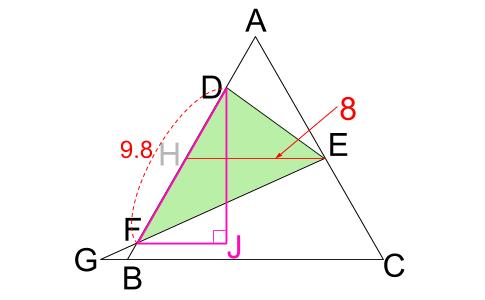
ピンク三角形 \(DFJ\) は三角定規型の有名三角形なので、\(DJ\) の長さが求まります。
\(DJ=9.8×\displaystyle \frac{\sqrt{3}}{2}\) です。
\(HE\) を内部底辺、\(DJ\) を高さとして、三角形 \(DEF\) の面積が求まります。
\(8×9.8×\displaystyle \frac{\sqrt{3}}{2}×\displaystyle \frac{1}{2}=\displaystyle \frac{98\sqrt{3}}{5}\)
求まりました!
(3)\(DE\) の長さ
求める長さ \(DE\) と関連する情報を集めましょう。
何か解決の糸口が見つかるはずです。
1.\(DE\) は(2)で面積を出した三角形 \(DEF\) の辺だから、面積から逆算ででそうだ。
2.しかも三角形 \(DEF\) の角 \(E\) の大きさ \(60°\) も使えそう。
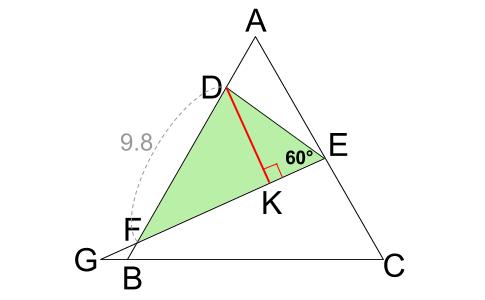
つまり、\(FE\) の長さがわかれば解決しそうです。
\(FE\) の長さの情報は・・・
\(FG:FE=1:4\) でしたね。前に出てきた砂時計相似(ピラミッド相似)です。
他には・・・?
問題文に書いてあって、まだ使っていないこと、(1)(2)を解いている途中で分かったこと、これらの中から、パズルを解くための鍵を探すしかありません。
答えは、
ずばり、
三角形 \(ADE\) と三角形 \(CEG\) の相似です。
一番はじめに注目した相似です。相似比は \(1:2\) なので、
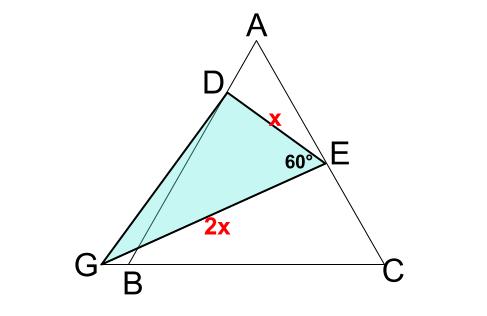
\(DE:EG=1:2\) です。
\(FG:FE=1:4\) と合わせると、下図のように長さをおけます。
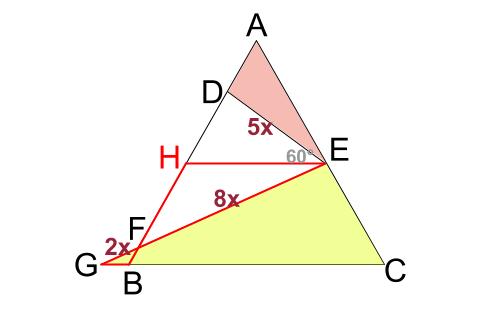
より、底辺が \(8x\) 、高さが \(5x×\displaystyle \frac{\sqrt{3}}{2}\) の三角形 \(DEF\) の面積が、\(\displaystyle \frac{98\sqrt{3}}{5}\) なので、
\(8x×5x×\displaystyle \frac{\sqrt{3}}{2}×\displaystyle \frac{1}{2}=\displaystyle \frac{98\sqrt{3}}{5}\)
整理すると、
\(x^2=\displaystyle \frac{49}{25}\)
\(x=\pm \displaystyle \frac{7}{5}\)
\(x\) は正なので、
\(x= \displaystyle \frac{7}{5}\)
求める長さ、\(DE=5x\) とおいたので、
\(DE=5x=7\)
以上求まりました!
別解1
さて、上の考察をしているとき、以下のことに気づいたでしょうか?
三角形 \(ADE\) と三角形 \(CEG\) から、相似比は \(1:2\) なので、
\(DE:EG=1:2\)
その間の角が \(60°\) なので・・・
三角形 \(GED\) は、正三角形を半分にした、三角定規型です!
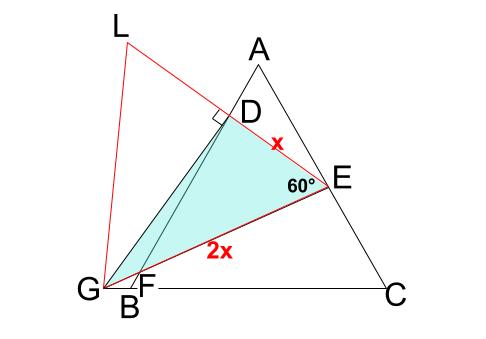
\(DEF×\displaystyle \frac{5}{4}=GED\)
\(GED×2=LGE\)
より、\(1\) 辺が \(2x\) の正三角形 \(LGE\) の面積は
\(\displaystyle \frac{98\sqrt{3}}{5}×\displaystyle \frac{5}{4}×2=49\sqrt{3}\)
\(1\) 辺が \(1\) の正三角形の面積は \(\displaystyle \frac{\sqrt{3}}{4}\) なので、
面積比は \(\displaystyle \frac{\sqrt{3}}{4}:49\sqrt{3}=\displaystyle \frac{1}{4}:49=(\displaystyle \frac{1}{2})^2:7^2\)
より、相似比は \(\displaystyle \frac{1}{2}:7\)
つまり、\(1:2x=\displaystyle \frac{1}{2}:7\)
よって、\(2x=14\)
\(x=7\)
\(DE=x=7\)
以上求まりました!
スポンサーリンク
