問題
下の図のような三角形に内接する円の半径を求めなさい。
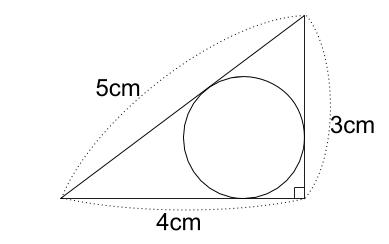
解答
超有名問題です。
\(2\) つの解き方を示します。
必ずどちらも理解・暗記しておきましょう。
解法1 円と接線の性質
円の中心と接点を結ぶ線分(半径)は、接線と垂直です。
そして、下図のような対称性があります。
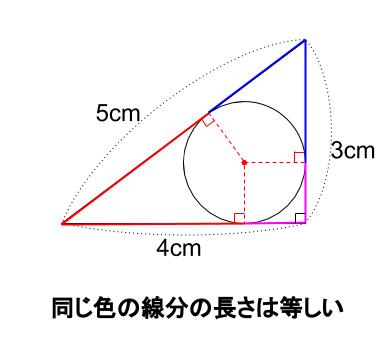
赤を \(x\)
青を \(y\)
ピンクを \(z\)
とすれば、
\(x+y=5\) ・・・①
\(x+z=4\) ・・・②
\(y+z=3\) ・・・③
となり、この連立方程式を解きます。
文字が \(3\) つの連立方程式の経験は少ないかもしれませんが、
大丈夫です。文字を消していくといういつものやり方です。
例えば、
②-③で、 \(z\) が消せます。
\(x-y=1\) ・・・④
①と④は、普通の連立方程式です。
\(x=3\)
\(y=2\)
と求まります。これと②より、
\(z=1\)
です。
そしてこれは、内接円の半径です。
右下の四角形は正方形ですから、ピンクの長さ \(1cm\) が
内接円の半径と等しいのです。
解法2 三角形の面積から
下図のように、\(3\) つの三角形に分割します。
円の中心と接点を結ぶと、すべて、各三角形の高さになります。
その高さはすべて共通で、内接円の半径 \(r\) と等しいです。
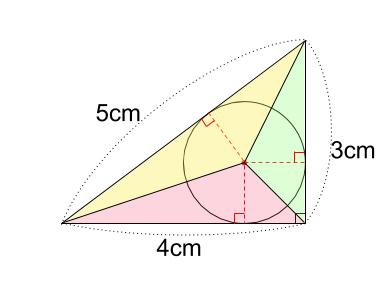
黄色の三角形の面積
\(5×r×\displaystyle \frac{1}{2}=\displaystyle \frac{5}{2}r\)
赤色の三角形の面積
\(4×r×\displaystyle \frac{1}{2}=\displaystyle \frac{4}{2}r\)
緑色の三角形の面積
\(3×r×\displaystyle \frac{1}{2}=\displaystyle \frac{3}{2}r\)
これら \(3\) つの合計は、全体の面積と等しいので、
\(\displaystyle \frac{5}{2}r+\displaystyle \frac{4}{2}r+\displaystyle \frac{3}{2}r=3×4×\displaystyle \frac{1}{2}\)
整理すると
\(\displaystyle \frac{5+4+3}{2}r=6\)
より
\(r=1\)
と求まります。
スポンサーリンク
