問題
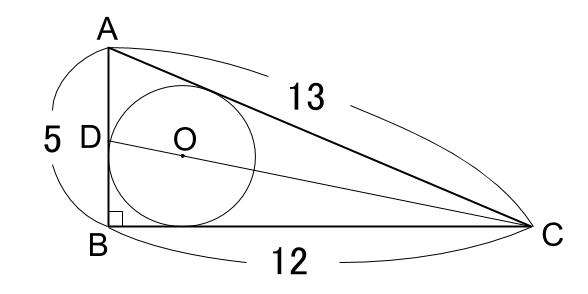
下図のように、直角三角形 \(ABC\) の内接円の中心を \(O\) とします。
線分 \(CO\) の延長線と \(AB\) の交点を \(D\) とします。このとき以下の問いに答えなさい。
(1)内接円の半径を求めなさい。
(2)\(AD\) の長さを求めなさい。
解説
(1)内接円の半径
内接円の半径の求め方は、別ページ にて解説をしています。
重要知識なので、知らない人は、まずはそちらを読んで学習しましょう。
本問における内接円の半径は、 \(2cm\) です。
(2)\(AD\) の長さ
2通りの解き方を紹介します。
相似の利用
内接円の中心 \(O\) から、各辺に下した垂線の長さは、半径 \(2cm\) です。
下図の、赤い小さい直角三角形と、クリーム色のの大きい直角三角形は相似です。
角度から明らかです(ピラミッド型相似とも言えます)。
相似比は、\(2:10=1:5\) です。
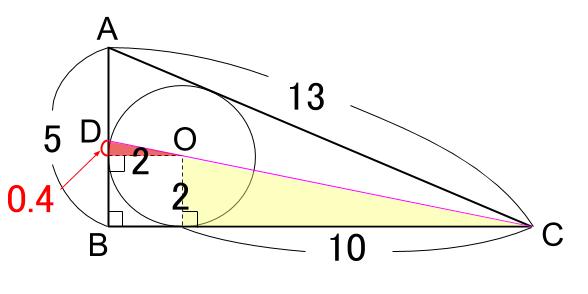
よって、上図の赤い小さい直角三角形の高さは
\(2×\displaystyle \frac{1}{5}=0.4\)
\(DB=2+0.4=2.4\)
求める \(AD\) の長さは、\(5-2.4=2.6\)
以上求まりました。
角の2等分と辺の比の利用
内接円と言えば「角の2等分」なのです。
これは、円と接線の図形的性質として絶対暗記しておかないといけないものです。
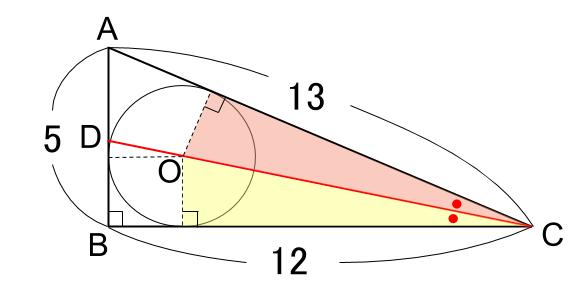
角の2等分線と辺の比の性質を暗記していれば、
\(AD:DB=13:12\)
より、\(AD=5×\displaystyle \frac{13}{13+12}=2.6\)
以上求まりました。
角の2等分線と辺の比の性質を知らない人は別ページにて説明があります。
角の2等分と線分の比のページ
スポンサーリンク
