問題
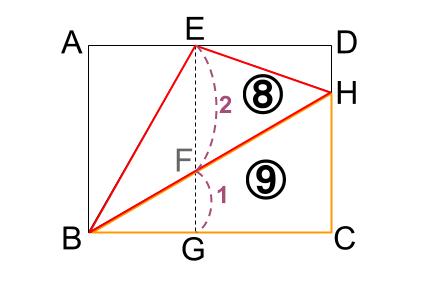
下図のように、線分\(BE,BH\) によって、長方形 \(ABCD\) の角 \(B\) が \(3\) 等分されています。\(EG\) と \(BC\) は垂直です。
三角形 \(EBH\) と三角形 \(HBC\) の面積比が \(8:9\) のとき次の問いに答えなさい。
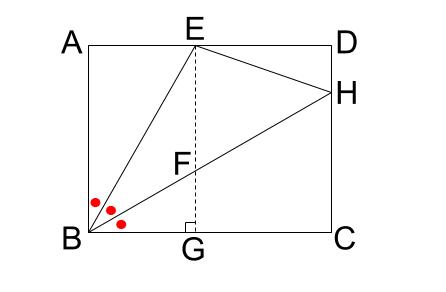
(1)\(EF:FG\) を求めなさい。
(2)\(DH:HC\) を求めなさい。
解説
(1) \(EF:FG\)
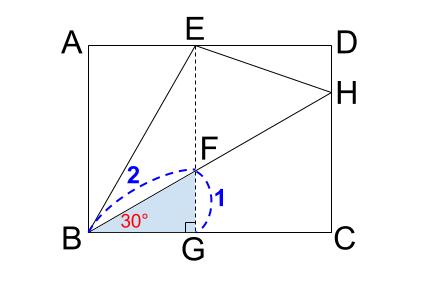
赤丸の角度は、直角の \(3\) 等分ですので、\(30°\) ずつです。
よって、三角形 \(FBG\) は正三角形を半分にした、有名三角形です。三角定規型です。
より、\(BF:FG\) は \(2:1\)
また、角度の考察をすると、三角形 \(FEB\) が二等辺三角形であることがわかります。
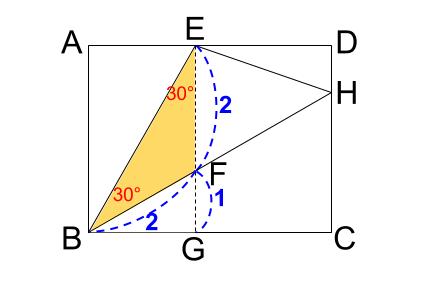
よって、\(EF:FG=2:1\)
求まりました!
参考
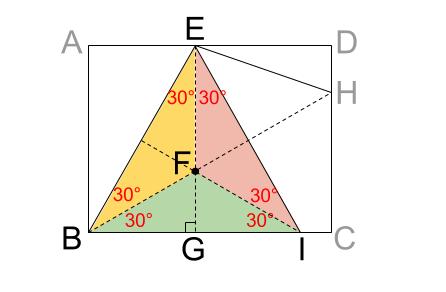
この図形配置は、正三角形の重心と関連しています。
下図の点 \(F\) を正三角形 \(EBI\) の重心といいます。
もちろん、\(EF:FG=2:1\) です。
(2)\(DH:HC\)
(2)を解くために、(1)の結論を使うことは非常に多いので、どう使うのかを考えます。
三角形 \(EBH\) と三角形 \(HBC\) の面積比が \(8:9\) ということですが、(1)の結論とどう結びつけるのか・・・
赤い三角形 \(EBH\) を \(FDA\) に等積変形します。
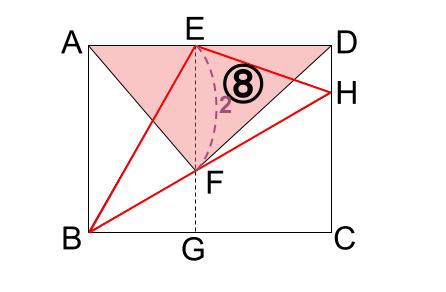
これで、面積 \(8\) と、\(EF\) の長さ \(2\) がつながりました。
※正確には長さの比ですが。
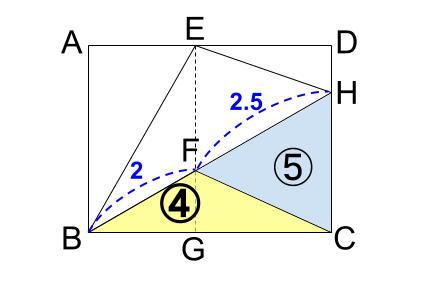
つまり、\(EF:FG=2:1\) は下図の面積比につながります。
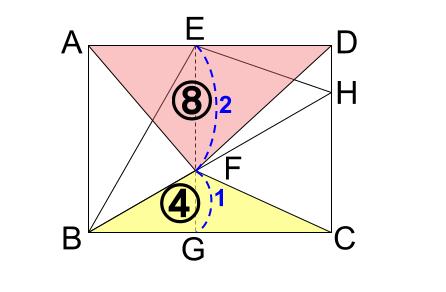
三角形 \(HBC\) の面積は \(9\) でしたから、水色の三角形 \(HFC\) の面積は \(9-4=5\)
ここで、\(BF,FH\) を底辺とみれば、高さの等しい \(2\) つの三角形の面積比が \(4:5\)
つまり、底辺の比も \(4:5\) です。
序盤に \(BF=2\) としたので、\(2:2.5\) と図には入れておきます。
※もちろん、ここから序盤の数字をかえて解いてもOKです。比を変化させなければ良いのです。
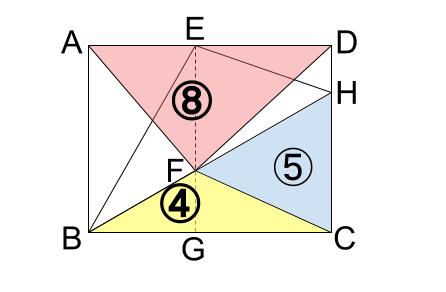
で、結局何が最終目標なのかと言えば・・・\(DH:HC\) です。
そろそろ、\(DH:HC\) に繋がりますね。
下図のようなピラミッド型相似です。
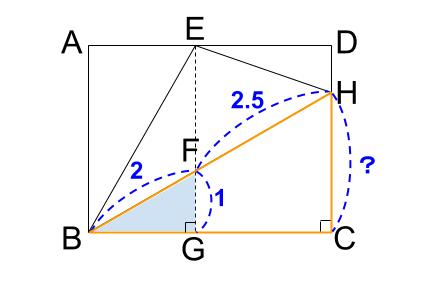
水色とオレンジの直角三角形が相似で、相似比は対応する辺からわかります。
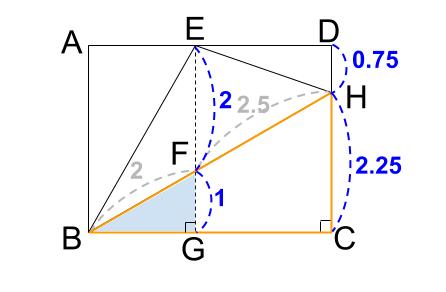
\(BF:BH=2:2+2.5=4:9\)
\(HC=FG×\displaystyle \frac{9}{4}=1×\displaystyle \frac{9}{4}=\displaystyle \frac{9}{4}=2.25\)
よって、\(DH=3-2.25=0.75\)
\(DH:HC=0.75:2.25=1:3\)
以上、求まりました!
スポンサーリンク
