問題
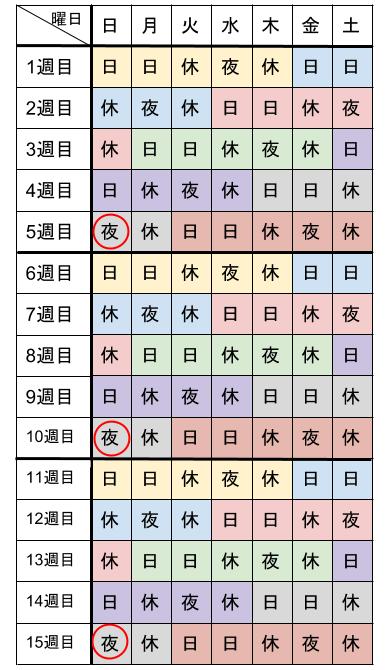
Aさんは、ある会社で勤務している。この会社では昼間に勤務する「日勤」、夜間に勤務する「夜勤」、そして「休み」の3種類の勤務形態があり、次のような順序をくり返して勤務することになっている。

Aさんは1週目の日曜日から勤務を開始した。したがって、Aさんの勤務表は表1のようになる。
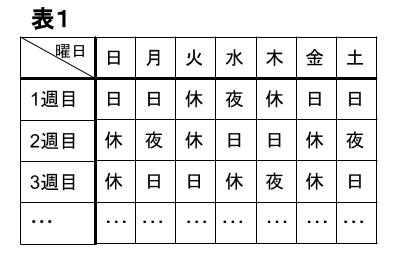
勤務を開始した日(1週目の日曜日)を1日目として、次の問に答えなさい。
(1)40日目は何曜日か、答えなさい。また、この日の勤務形態は日勤、夜勤、休みのどれになるか、答えなさい。
(2)n回目の夜勤が何日目であるか、勤務開始からの日数を調べたところ、表2のようになることがわかった。
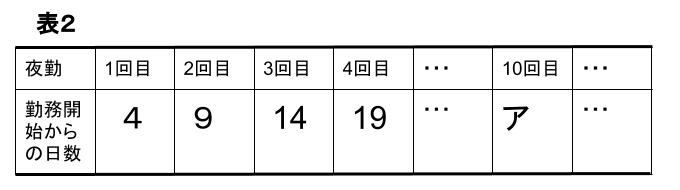
① 表2のアにあてはまる数を求めなさい。
②n回目の夜勤は何日目であるか、nを用いた式で表しなさい。
(3)日曜日が夜勤になる日について。
①はじめては何日目ですか。 29日目
②3回目は何日目ですか。 29+35+35=99日目
解説
(1)40日目は何曜日?
曜日は、7ずつの周期。
よって、7で割ったときのあまりで分類されます。
40÷7=5あまり5
より、40日目は木曜日です。
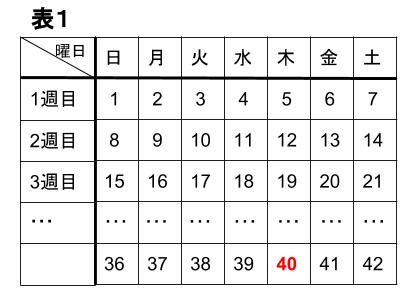
ちなみに、
日曜日は、7で割ったときのあまり1
月曜日は、7で割ったときのあまり2
火曜日は、7で割ったときのあまり3
水曜日は、7で割ったときのあまり4
木曜日は、7で割ったときのあまり5
金曜日は、7で割ったときのあまり6
土曜日は、7で割ったときのあまり0、あまりなし。
次に、勤務形態ですが、これは5ずつの周期。
よって、5で割ったときのあまりで分類されます。
40÷5=8
つまり、あまり0です。
よって、40日目は休みです。

(2)②10回目の夜勤
表2を再掲します。
このアを求めるのです。

これは(1)で使った表の一部なのです。
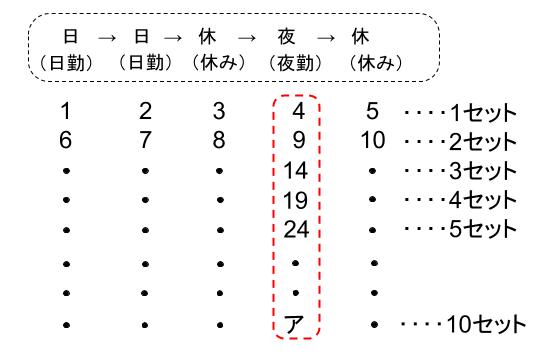
アの求め方は2通り紹介します。
4、9、14・・・
という数の列は、5ずつ足すことで次の数になる列です。
10番目は、はじめの4に5を9回足した数になるので、
4+5×9=49
より、ア=49と求まります。
別解
別解は、5ずつの周期であることを利用して、5の倍数に着目します。
下の表の、5の倍数が並ぶ列に着目するのです。
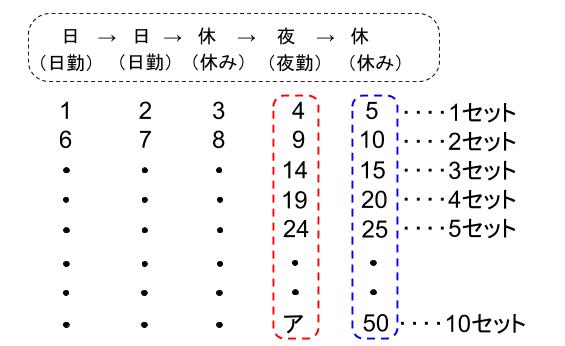
青い列には、5の倍数が並ぶので、アの右隣の数は、
5×10=50
より、アは50のひとつ前、49と求まります。
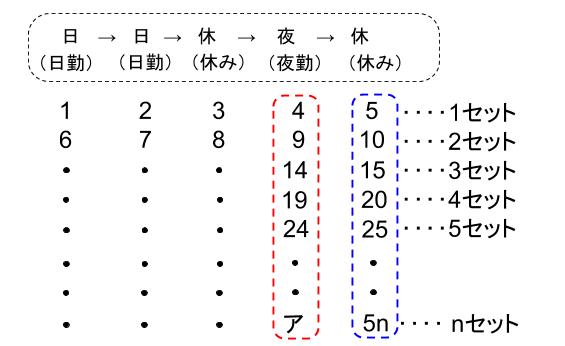
(2)②n回目の夜勤は何日目であるか、nを用いた式で表せ。
①と同様に解きます。
4、9、14・・・
という数の列は、5ずつ足すことで次の数になる列です。
n番目は、はじめの4に5を(n-1)回足した数になるので、
4+5×(n-1)=4+5n-5
=5n-1
より、5n-1日目と求まります。
別解も①と同様です。
n個目の5の倍数は、5n
より、5nのひとつ前、5n-1と求まります。
(3)日曜日が夜勤になる日について。
①はじめては何日目ですか。
②3回目は何日目ですか。
曜日は、7ずつの周期。
勤務形態は、5ずつの周期。
この2種類の周期を合わせた周期の問題です。
このようなときは、最小公倍数です。
7と5の最小公倍数は35、よって、35ずつの周期となります。
ずばり図をかいて、目で見て確かめましょう。
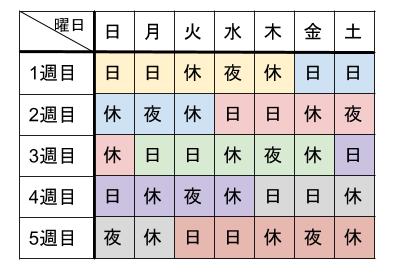
この35日間で、1セットとなります。
6週目からは、1週目からと同じようにくりかえされていきます。
この表を見て答えを出します。
はじめて日曜日が夜勤になる日は、29日目です。
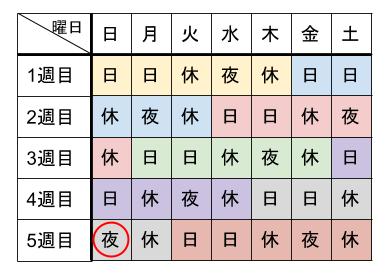
3回目に日曜日が夜勤になる日は、3セット目の同じ日なので、
35+35+29=99
より、99日目です。