角の2等分と線分の比
知っておくと役に立つ以下の定理があります。
下図のように、角 \(A\) の \(2\) 等分線と、\(BC\) の交点を \(D\) とします。
このとき、\(BD:DC=AB:AC\)

一応、中学数学の範囲外なので、頻繁に出題されるものではありませんが、知っていることで有利になることもあります。極めて覚えやすい定理なので、覚えておいて損はありません。
角の2等分と線分の比の証明
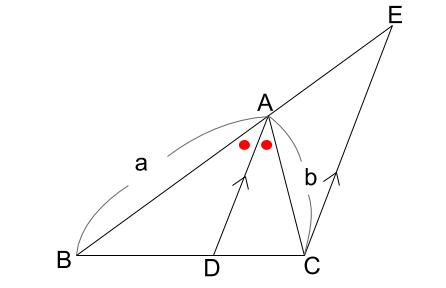
下図のように、\(AD\) と平行な線分 \(EC\) を引きます。
いわゆるピラミッド型相似ができます。
また、平行線の錯角より、\(\angle DAC=\angle ECA\)
また、平行線の同位角より、\(\angle BAD=\angle AEC\)
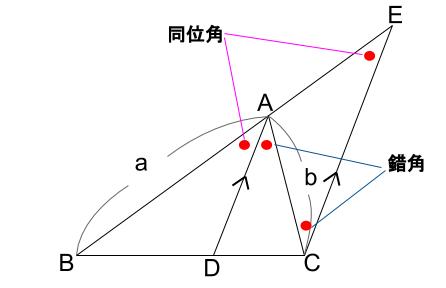
このことから、三角形 \(ACE\) は、二等辺三角形です。
したがって、\(AC=AE=b\)
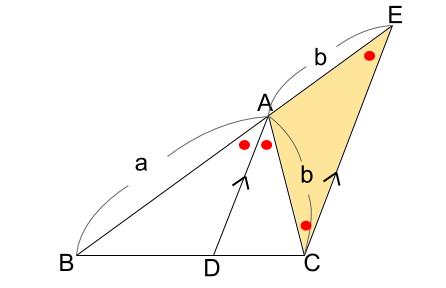
さて、ピラミッド型相似に注目しましょう。
\(BA:AE=a:b\) ですので、
\(BD:DC=a:b\) も成り立ちます。
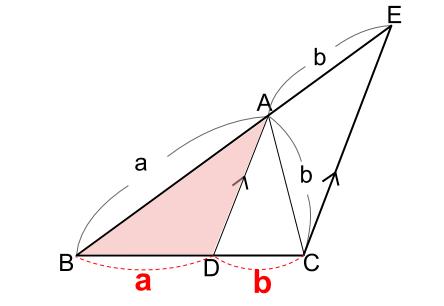
以上で証明終了です。
中学数学の範囲外、と書きましたが、範囲外なのか範囲内なのかは曖昧です。
上の証明は、中学生でも容易に理解できるからです。
また、この定理の証明そのものが、誘導つきで出題されることもあります。
例題1
下の図において、\(AD\) は角 \(A\) の \(2\) 等分線です。
\(BD\) の長さを求めなさい。
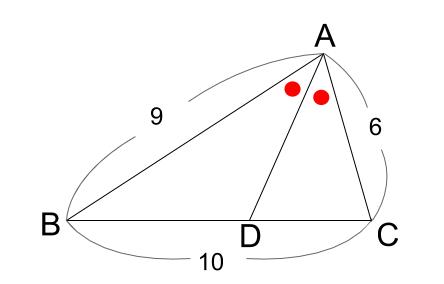
解説
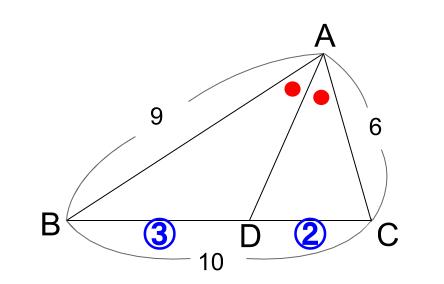
角の \(2\) 等分と線分の比の性質を使うのみです。
\(BD:DC=9:6=3:2\) なので、
\(BD=10×\displaystyle \frac{3}{3+2}=6\)
以上、求まりました。
例題2
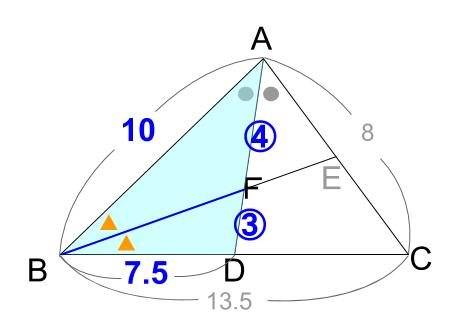
下の図において、\(AD\) は角 \(A\) の \(2\) 等分線であり、\(BE\) は角 \(B\) の \(2\) 等分線です。
\(AF:FD\) を求めなさい。
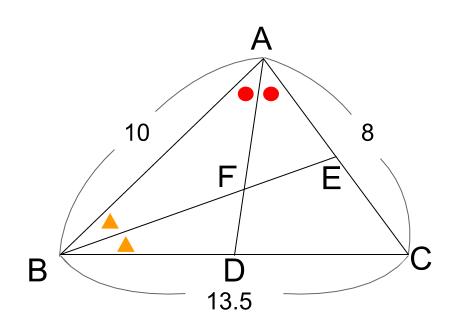
解説
角の \(2\) 等分があるので、線分の比が求められます。
角の \(2\) 等分と線分の比の性質を使いましょう。
角 \(A\) の\(2\) 等分線より、
\(BD:DC=10:8=5:4\)
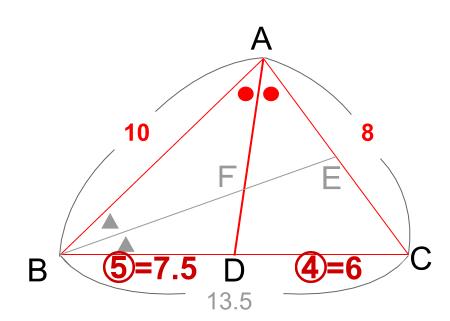
\(BD=13.5×\displaystyle \frac{5}{5+4}=7.5\)
次に、角 \(B\) の\(2\) 等分線より、
\(AF:FD=10:7.5=4:3\)
以上求まりました。
スポンサーリンク
