問題
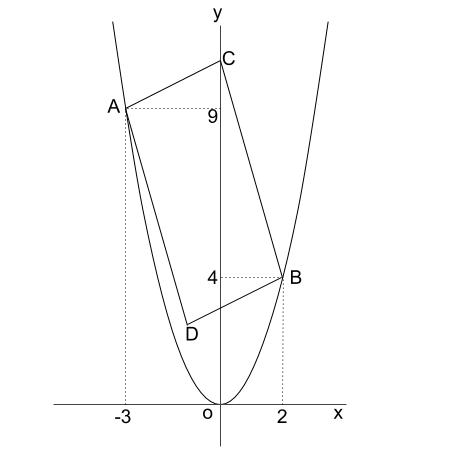
下図において、関数 \(y=x^2\) のグラフ上に \(2\) 点 \(A,B\) があり、
点 \(A(-3,9)\) 、点 \(B(2,4)\) である。
\(y\) 軸上に点 \(C\) をとり、四角形 \(ADBC\) が平行四辺形になるように
点 \(D\) をとります。平行四辺形 \(ADBC\) の面積が \(24\) となるとき、
点 \(D\) の座標を求めなさい。
ただし、点 \(C\) の \(y\) 座標は、点 \(A\) の \(y\) 座標より大きいものとする。
解説
この平行四辺形の面積を、「底辺×高さ」から求めようとするのは
無謀ですね。
下のように、よく知った三角形 \(2\) つに分けるのが楽なパターンです。
\(AB\) を通る直線の式が \(y=-x+6\) と簡単に求まるので、
この直線の \(y\) 切片は \(6\) です。
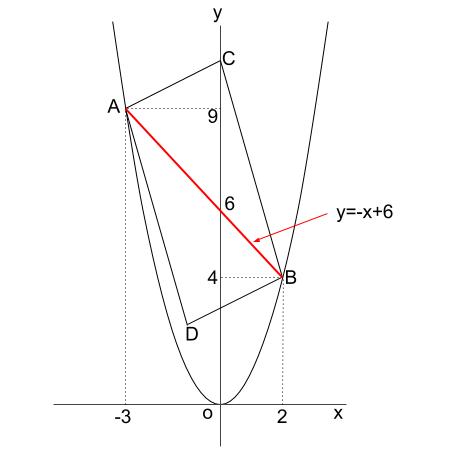
ちなみに、この \(6\) は、下図のように、相似を用いて図形的に求めてもかまいません。
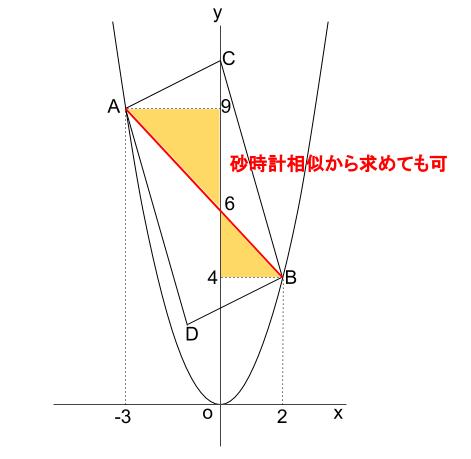
さて、
面積が \(24\) である平行四辺形 \(ADBC\) が、合同な\(2\) つの三角形に割れました。
処理しやすいのはもちろん、三角形 \(ABC\) の方ですね。
その面積は \(12\) です。
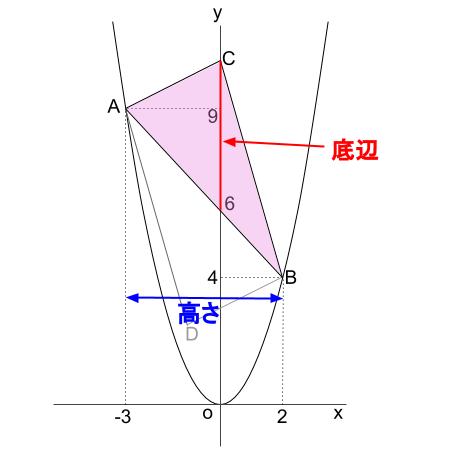
この三角形の面積は、赤い線分を底辺(内部底辺とも言う)とし、
高さが \(5\) として求められます。
よって、
\(赤い線分×5×\displaystyle \frac{1}{2}=12\)
\(赤い線分=4.8\)
よって、\(C\) の \(y\) 座標は \(6+4.8=10.8\) です。
いよいよ \(D\) です。
平行四辺形の対称性から、下図の黄色い直角三角形は合同です。
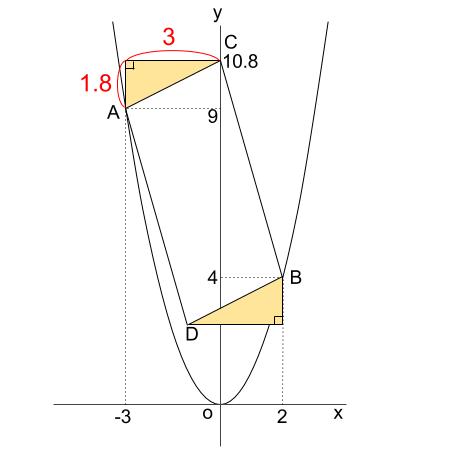
\(A,C\) の座標から、直角三角形の辺の長さはわかります。
たてが \(1.8\)
よこが \(3\) です。
よって、\(B(2,4)\) から \(D\) の座標が求まります。
\(D(2-3,4-1.8)\)
つまり、
\(D(-1,2.2)\)
これが求める座標です。
スポンサーリンク
