円に内接する四角形の性質

円に内接する四角形

円に内接する四角形の性質は、高校数学の範囲ですが、中学生も知っておくと便利です。
それに、中学生が学習してもなんなく習得できます。簡単です。

例１

下の図で、角 $x$ を求めなさい。

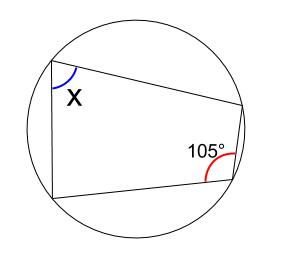
解答

円に内接する四角形の性質より、

$180-105=75$

より、75度
これでＯＫです。

円に内接する四角形の性質の証明

なぜ上の性質が成り立つのか。
中学生でも簡単にわかります。

説明１　円周角の定理より

下図のように、円周を２つの弧に分けます。
赤い弧と青い弧です。これらを合わせると円周全体になります。

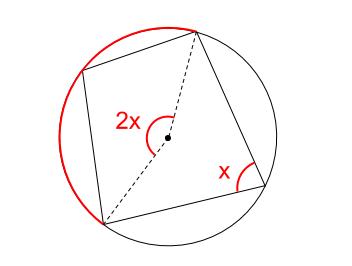
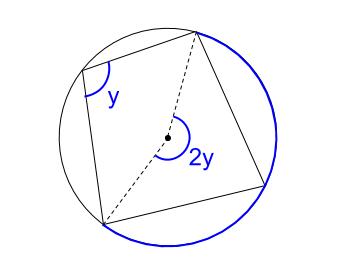
中心角より、$2x+2y=360°$
この式を $2$ で割れば、
$x+y=180°$
これは、対角の和が $180°$ であることを示しています。
以上、証明できました。

説明２　中心から補助線

円があれば、その中心から補助線を引きます。
そうすれば、図形的性質が明らかになります。
あらゆるときに活用する代用的な補助線ですね。

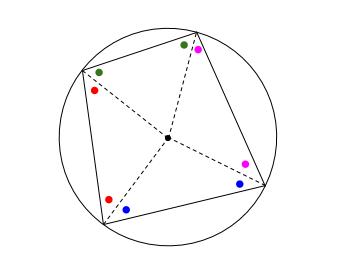
半径を辺とする二等辺三角形が $4$ つできます。
各色すべての角を $2$ つずつ足すと、四角形の内角の和であり、 $360°$ です。
つまり、その半分、各色すべてを $1$ つずつ足すと、$180°$ です。

向いあう角の色を見ると、各色すべての角が $1$ つずつになっています。

以上、示せました！

例題１

下の図において、角 $x$ を求めなさい。

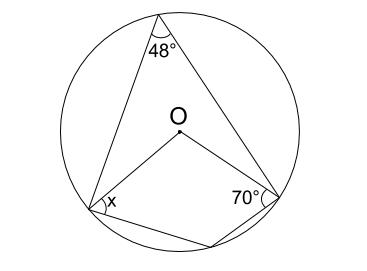
解説

円に内接する四角形の性質を知らなくとも解けるのですが・・・

もちろん、円周角の定理です。

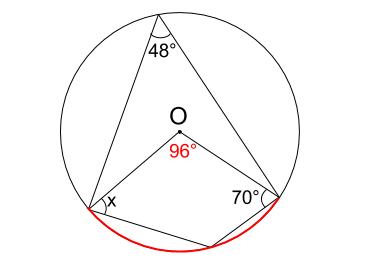
赤い弧の円周角 $48$ 度の $2$ 倍が中心角なので、中心角は
$48×2=96°$

$96°$の逆は、$360-96=264°$
これは青い弧の中心角なので、青い弧の円周角は、
$264÷2=132°$

最後は四角形の内角の和より、
$360-(70+96+132)=62°$

以上求まりました！

内接四角形の性質を知っていれば、青い弧の円周角 $132°$ を求めるさい、
$180-48=132°$
で解決します。
少し近道ができますね！

スポンサーリンク