問題
下の図のように、線分 \(AB\) を直径とする半円があり、点 \(O\) は \(AB\) の中点である。
\(\stackrel{ \Large \frown }{ AB }\) 上に、点 \(C\) 、点 \(D\) をとり、線分 \(AD\) と \(BC\) の交点を \(E\) とする。また、点 \(C,D\) を結ぶ。
次の問いに答えなさい。
(1)\(\triangle EDC \backsim \triangle EBA\) を証明しなさい。
(2)\(\stackrel{ \Large \frown }{ AD }:\stackrel{ \Large \frown }{ DB }=2:1\)
\(\angle DBC=45°,OA=2cm\) とする。このとき、三角形 \(EDC\) の面積を求めなさい。
解説
(1)\(\triangle EDC \backsim \triangle EBA\)
明らかに、「\(2\) つの角が等しい」から相似を示すします。
円周角の定理より示せますね。
同じ色の丸は、円周角の定理より等しいことがいえます。
また、対頂角も等しいです。
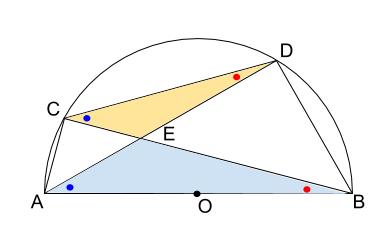
この証明は基本なので、省略します。
(2)三角形 \(EDC\) の面積
\(\stackrel{ \Large \frown }{ AD }:\stackrel{ \Large \frown }{ DB }=2:1\)
\(\angle DBC=45°,OA=2cm\)
という与えられた情報を図にかきこみます。
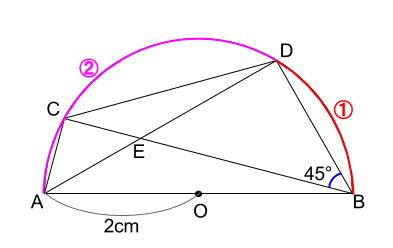
ここから、直径があるので円周角の \(90°\) にはすぐ気付けます。
※正確には半円の弧の円周角は \(90°\)
対頂角で \(45°\)
など、すぐにわかる情報を追加します。
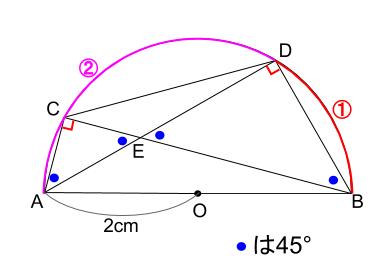
これ以上進みませんので、まだ使っていない情報、
\(\stackrel{ \Large \frown }{ AD }:\stackrel{ \Large \frown }{ DB }=2:1\)
をどのように利用するのか考えましょう。
弧の長さの比なので、円周角や中心角の比として使うしかありません。
半円の弧を \(2:1\) に分けているので、中心角 \(180°\) を \(2:1\) にわけます。
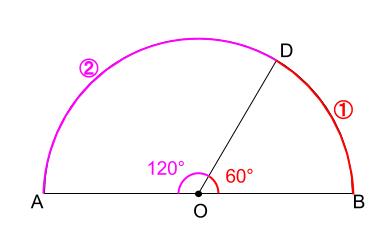
よって、
\(\stackrel{ \Large \frown }{ AD }\) の円周角は \(120°\) の半分の \(60°\)
\(\stackrel{ \Large \frown }{ DB }\) の円周角は \(60°\) の半分の \(30°\)
下図のようになります。
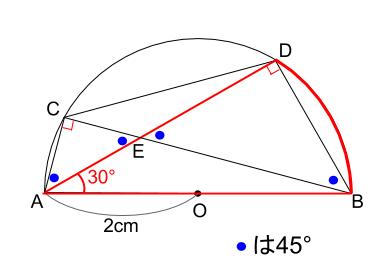
よって、三角形 \(ADB\) が\(30°,60°,90°\) の三角定規型であることがわかります。
辺の比は \(2:1:\sqrt{3}\) なので、
\(BD=2cm\)
\(DA=2\sqrt{3}cm\) です。
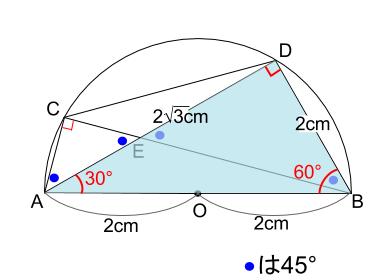
あとは、\(2\) つの直角二等辺三角形を用いれば解けます。
\(AE=2\sqrt{3}-2\) です。
また、\(AE\) の中点を \(M\) とすれば
直角二等辺三角形 \(AEC\) は下図のように、\(CM\) で二等分されます。
分かれた図形も、直角二等辺三角形です。
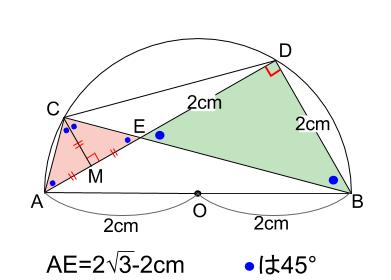
上図から、\(CM=AM=EM=(2\sqrt{3}-2)×\displaystyle \frac{1}{2}=\sqrt{3}-1\) が得られます。
この \(CM=\sqrt{3}-1\) こそが、最終目標である三角形 \(EDC\) の高さです。
三角形 \(EDC\) は、
底辺が \(ED=2\) で
高さが \(CM=\sqrt{3}-1\)
なので、その面積は、
\(2×(\sqrt{3}-1)×\displaystyle \frac{1}{2}=\sqrt{3}-1(cm^2)\)
これが求める答えとなります。
(2)三角形 \(EDC\) の面積の別解
(1)で \(\triangle EDC \backsim \triangle EBA\) を示しています。
この相似比と面積比でも解答可能です。
相似比は、 \(1:\sqrt{2}\)
より面積比 \(1:2\)
\(\triangle ADB\) から \(\triangle DEB\) を引いて、\(\triangle EBA\) の面積は \(2\sqrt{3}-2\)
三角形 \(EDC\) の面積は、三角形 \(EBA\) の面積の半分なので、\(\sqrt{3}-1\)
スポンサーリンク
