問題
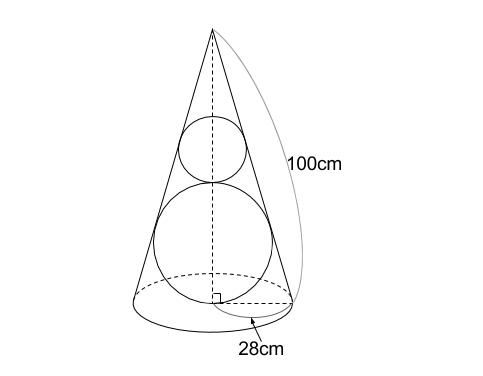
下の図のように、底面の半径が \(28cm\),母線の長さが \(100cm\) の円錐に
\(2\) つの球が内接しています。球と球も接しています。
このとき、小さい球の半径を求めなさい。
解説
円錐と内接球・その1の追加問題です。
下の大きい球の半径は、
問題1と完全に同じ求め方により、\(21cm\) と求まります。
ここまで求めた状態から、次に上の小さい球の半径を求めます。
下の図のようになっています。
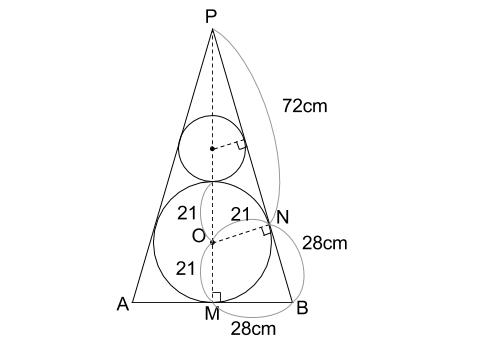
この図における相似な直角三角形たちは、 \(3\) 辺の比が \(25:24:7\) であり、
下図の水色の直角三角形も\(3\) 辺の比が \(25:24:7\) です。
青い長さは求める半径で、その長さが \(7\)(⑦)
赤い長さは \(25\) (㉕)です。
\(25+7=32\) (㉜)が、\(96-21×2=54(cm)\) です。
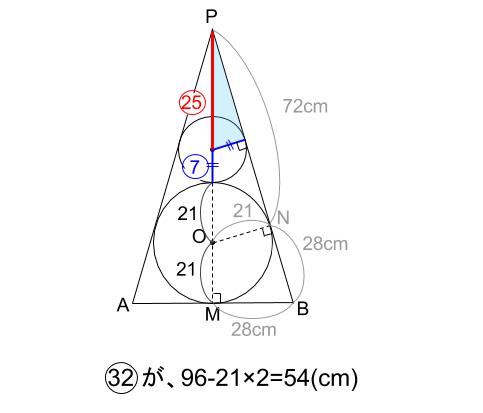
\(54cm\) を \(25:7\) に比例配分します。
\(54×\displaystyle \frac{7}{25+7}=×\displaystyle \frac{189}{16}(cm)\)
これが、求める小さい球の半径です。
別解
別の部分の相似に着目する解法もあります。
下図のように相似になっています。
「三角形と内接円、合わせた図形」どうしが相似です。
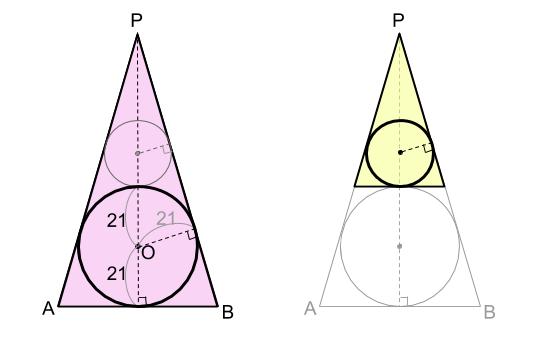
左の三角形の高さは、\(96cm\)
右の三角形の高さは、\(96-21×2=54(cm)\)
つまり、相似比は \(96:54=16:9\) です。
よって、内接円の相似比も \(16:9\) なので
\(21×\displaystyle \frac{9}{16}=×\displaystyle \frac{189}{16}(cm)\)
これが、求める小さい球の半径です。
スポンサーリンク
