問題
赤、白、青の3種類の長方形のカードを、次の手順にしたがって並べて長方形を作る。このとき、あとの問いに答えなさい。ただし、3種類のカードの縦の長さはすべて6cmで、横の長さは、赤は1cm、白は3cm、青は5cmである。
手順
「1番の長方形」は赤のカードを置く。

「2番の長方形」は「1番の長方形」の右端にすき間がないように、白のカードを並べて作る。
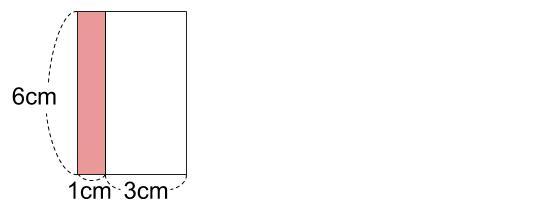
「3番の長方形」は「2番の長方形」の右端にすき間がないように、青のカードを並べて作る。
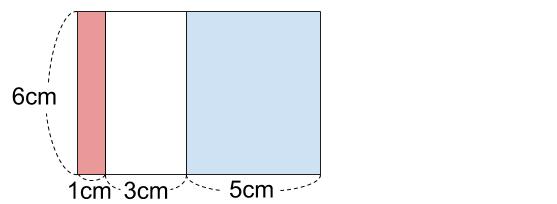
「4番の長方形」は「3番の長方形」の右端にすき間がないように、赤のカードを並べて作る。
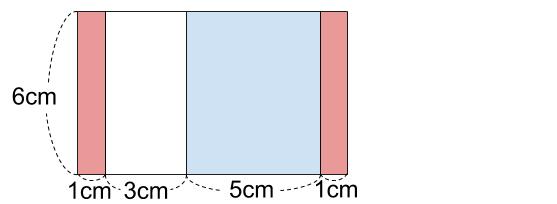
以下、同様に、「N番の長方形」は「(N-1)番の長方形」の右端にすき間がないように、カードを並べて作ります。カードの色は、赤、白、青、赤、白、青・・・の順です。
(1)「17番の長方形」を作ったとき、一番右端に並べたカードの色は何か求めなさい。
(2)「22番の長方形」の横の長さを求めなさい。
(3)一番右端に赤色のカードを並べて作った長方形で、使った赤のカードの総数が \(n\) 枚であるとき、この長方形の面積を \(n\) を使った式で表しなさい。
解説
(1)「17番の長方形」の右端の色
赤、白、青の3つ周期です。
「周期」は問題を解くための最重要のカギとなります。
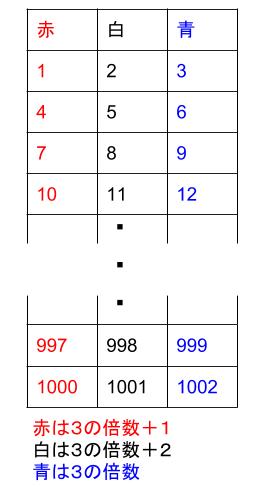
左から何枚目が何色なのかを表にすると下のようになります。
周期3なので、3個で1列の表になります。
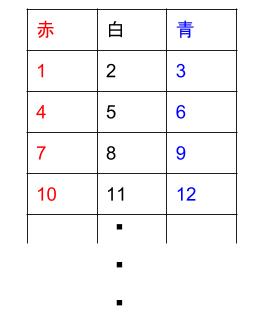
と続きます。
17までかき出すことも容易いですね。
答えは白です。
ところで、「1000番の長方形」の右端の色を求めるとしたら・・・
かき出して求めるのはいやですね。
計算で求める方法は、表をたてに見ます。
これは、3で割ったときのあまりで分類されているのです。
赤は3で割ると1余る数
白は3で割ると2余る数
青は3で割ると0余る数、つまり割り切れる数
より、「1000番の長方形」の右端の色は、
1000÷3=333あまり1
より、赤です。あまりが1なので、赤なのです。
(2)「22番の長方形」の横の長さ。
これも周期の利用です。「赤白青」と3枚並べると、横の長さは、1+3+5=9 \(cm\) です。これを1セットとします。
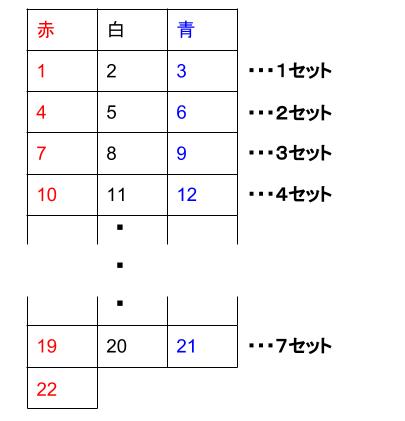
21枚目の青までで、21÷3=7
より、7セットあります。
つまり、「赤白青」の9 \(cm\) が7セットと、最後に赤の1cmが1枚です。
より、9×7+1=64 \(cm\) です。
(3)一番右端が赤色で赤のカードの総数が \(n\) 枚であるとき、この長方形の面積
赤1枚のとき横は、1cm
赤2枚のとき横は、(1+3+5)+1=10cm
赤3枚のとき横は、(1+3+5)+(1+3+5)+1=19cm
より、9cmずつ増えます。
等差数列といいます。
赤が \(n\) 枚のとき横の長さは、
(1+3+5)×(n-1)+1=9(n-1)+1=9n-8(cm)
このときの長方形の面積は、
6×(9n-8)
これで求まりました。
スポンサーリンク
