問題
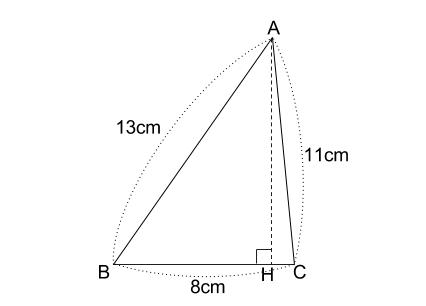
下の図のように、\(AB=13cm,BC=8cm,CA=11cm\) の三角形 \(ABC\) があります。
\(AH\) と \(BC\) が垂直のとき、\(AH\) の長さを求めなさい。
解説
中学数学において、求めたいものを \(x\) とおくことが
常套手段です。
しかし、この問題で \(AH=x\) とおくと・・・
\(x\) だけで立式すると、その後の計算は地獄です(中学生には無理)。
ですから自然に、\(BH=y\) とおきたくなりますよね。
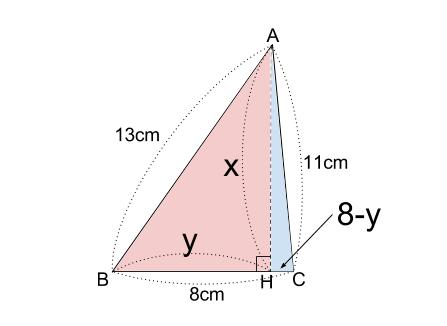
つまり、左の赤い三角形に三平方の定理を用いて
\(13^2=x^2+y^2\) ・・・①
また、右の青い三角形に三平方の定理を用いて
\(11^2=x^2+(8-y)^2\) ・・・②
①、②を連立させますが、
\(x\) を消す方が楽ですね。
最終的に \(x\) を求めたいのですが、まずは\(y\) の方程式にして、
\(y\) を求めるというわけです。
①ー②より、
\(169-121=y^2-(8-y)^2\)
\(48=16y-64\)
\(16y=112\)
\(y=7\)
あとは、①式に \(y=7\) を代入して
\(x^2=13^2-7^2\)
\(x^2=120\)
\(x=\pm \sqrt{120}\)
\(x=\pm 2\sqrt{30}\)
\(x\) は \(0\) より大きいので、
\(x= 2\sqrt{30}\)
これが求める長さです。
スポンサーリンク
