問題
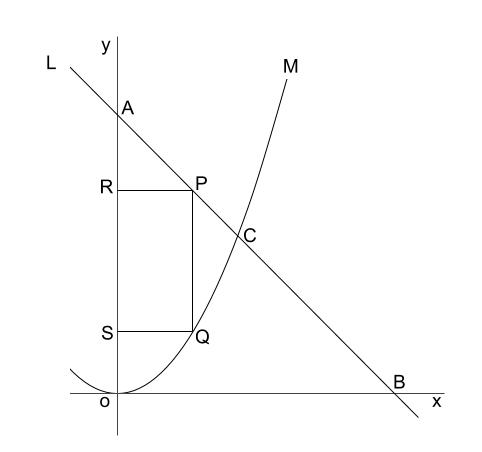
直線 \(L\) は一次関数 \(y=-x+8\) のグラフであり、直線 \(L\) と \(y\) 軸の交点を \(A\)、直線 \(L\) と \(x\) 軸の交点を \(B\) とする。
直線 \(L\) 上の点 \(C\) の座標は \((4,4)\) であり、点 \(C\) を通る関数 \(y=\displaystyle \frac{1}{4}x^2\) のグラフが \(M\) である。
点 \(P\) は線分 \(AC\) 上にあり、点 \(A,C\) のいずれにも一致しない点とする。
点 \(P\) を通り \(y\) 軸と平行な直線を引き、曲線 \(M\) との交点を \(Q\) 、
点 \(P\) を通り \(x\) 軸と平行な直線を引き、 \(y\) 軸との交点を \(R\)、
点 \(Q\) を通り、 \(x\) 軸に平行な直線を引き、 \(y\) 軸との交点を \(S\) とします。
長方形 \(PRSQ\) が正方形になるとき、点 \(P\) の \(x\) 座標を求めなさい。
解説
まず問題の意味をしっかりと掴みましょう。
要は、 点 \(P\) が \(AC\) 上を動くと、
連動して 長方形 \(PRSQ\) の形が変化する!
ということですね。
求めたいものを文字でおき、等式をたてる。
あとは方程式を解く。
これが中学数学の王道です。
点 \(P\) の \(x\) 座標を \(t\) とおいてみましょう。
すると、いろいろな値が \(t\) で表現できます。
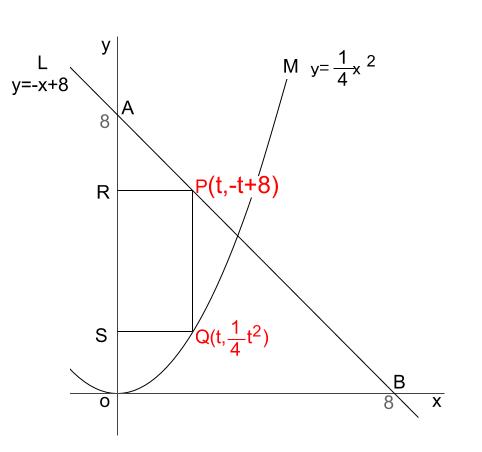
点 \(P\) は \(y=-x+8\) 上の点なので、 \(y\) 座標は、 \(-t+8\)
点 \(Q\) の \(x\) 座標は、点 \(P\) と同じ \(t\) で、
点 \(Q\) は \(y=\displaystyle \frac{1}{4}x^2\) 上の点なので \((t, \displaystyle \frac{1}{4}t^2)\) となります。
これで、長方形 \(PRSQ\) の縦の長さと横の長さを \(t\) の式で表せます。
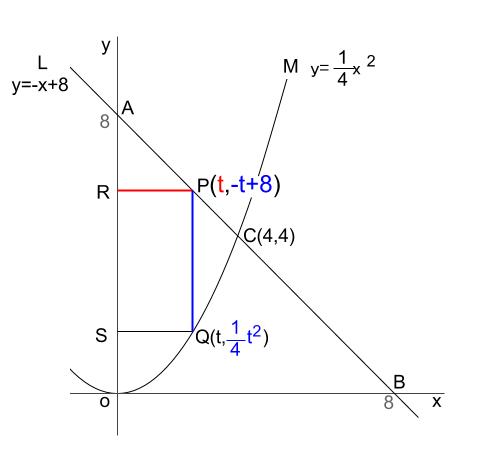
縦の長さは点 \(P,Q\) の \(y\) 座標からわかります。
\(縦の長さ=-t+8-\displaystyle \frac{1}{4}t^2\)・・・①
横の長さは点 \(P\) の \(x\) 座標からわかります。
\(横の長さ=t\)・・・②
長方形 \(PRSQ\) が正方形になるとは、
縦と横が同じ長さになるときなので、①、②より
\(-t+8-\displaystyle \frac{1}{4}t^2=t\)
あとは、この方程式を解くだけです。
これを解くと
\(t=-4 \pm 4\sqrt{3}\)
となりますが
\(0 \lt t \lt 4\) なので
\(t=-4 + 4\sqrt{3}\)
これが、求める点 \(P\) の \(x\) 座標です。
スポンサーリンク
