問題
赤色、青色、白色の同じ大きさの正方形のカードがたくさんある。下の図のように、これらのカードを次の規則にしたがって正方形状に並べていく。
規則
・はじめに赤色のカードを1枚並べる。これを1回目の操作とする。
・2回目の操作は、1回目の操作で並べたカードの外側に、青色のカードを3枚並べる。
・3回目の操作は、2回目の操作で並べたカードの外側に、白色のカードを5枚並べる。
・4回目の操作は、3回目の操作で並べたカードの外側に、赤色のカードを7枚並べる。
以下、5回目は青色のカードを9枚、6回目は白色のカードを11枚、・・・のように、赤色、青色、白色のカードの順でくり返し並べていく。
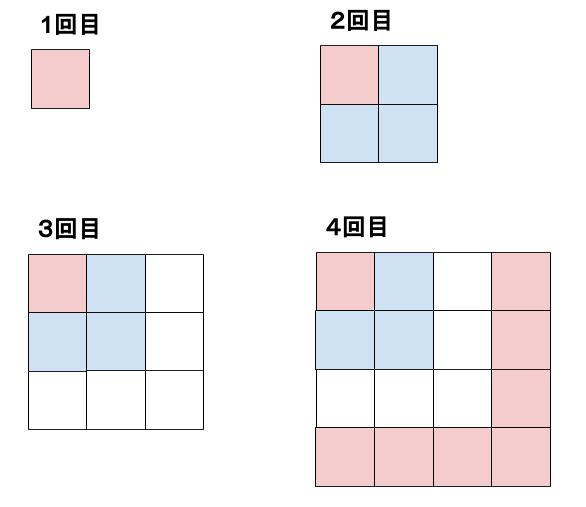
このとき、次の問いに答えなさい。
(1)10回目の操作で並べるカードは何枚か。
(2)何回目かの操作後、正方形状に並んでいるカードは全部で144枚であった。このとき、最後に並べたカードは何色か。
(3)カードを並べた順番をそのカードの番号とする。n回目の操作において、最初に並べるカードの番号をA、n番目に並べるカードの番号をB、最後に並べるカードの番号をCとする。例えば、4回目の操作後に並んでいるカードの番号は、A=10、B=13、C=16である。このとき、次の①②に答えよ。ただし、nは2以上の整数とする。
① Bをnの式で表せ。
②ABCの間には「AとBとCの和は、3の倍数になる」という関係が成り立つ。このことをnを用いて証明せよ。ただし、証明は結論だけでなく、考え方の過程がわかるように、途中の式なども書くこと。
解説
(1)10回目の操作で並べるカードは何枚か。
9回目の操作をすると、1辺が9の正方形ができます。
9回目までに、9×9=81、全部で81枚のカードを並べました。
10回目の操作をすると、1辺が10の正方形ができます。
10回目までに、10×10=100、全部で100枚のカードを並べました。
つまり、10回目の操作では、100-81=19
より、19枚のカードを並べました。
別解
1回目に1枚
2回目に3枚
3回目に5枚
4回目に7枚
となっていて、1,3,5,7・・・は奇数の列です。
n回目に2n-1枚並べるので、
10回目に、2×10-1=19、
より、19枚並べます。
参考知識
奇数の列の和は、平方数になります。
1
1+3=4
1+3+5=9
1+3+5+7=16
1+3+5+7+9=25
以下続く。
(2)全部で144枚並べたときの、最後に並べたカードの色。
144=12×12
※暗記していますよね!?
つまり、12回目の操作後です。
最後の操作、つまり12回目の操作のときのカードの色を求めます。
カードの色は3周期です。
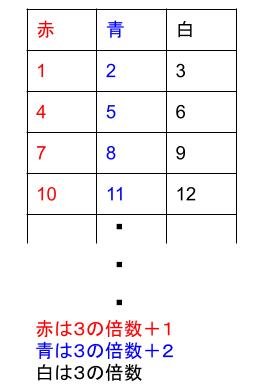
より、12回目の操作のときのカードの色は白色です。
※3で割ったときのあまりで分類されます。
例えば100回目の操作で並べる色は、100=3×33+1より、赤色です。
(3)①Bをnの式で表せ。
Cは平方数となります。
n回目の操作が終わったとき、1辺がnの正方形が完成します。
1辺がnの正方形には、\(n^2\) 枚の小正方形を並べていて、最後がCとなります。
つまり、\(C= n^2\) になります。
そして、BはCから(n-1)引いた値になります。
より、\(B=n^2-(n-1)=n^2-n+1\)
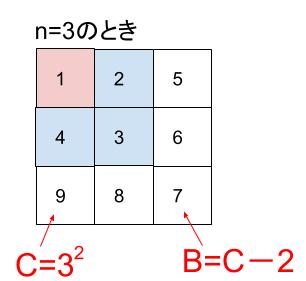
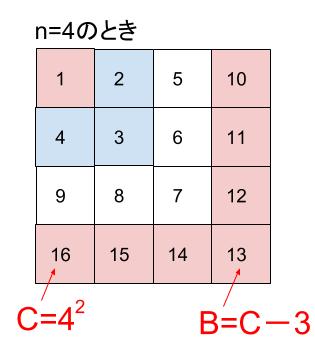
②「AとBとCの和は、3の倍数になる」このことをnを用いて証明せよ。
①より、
\(C= n^2\)
\(B=n^2-n+1\)
である。
あとは、Aをnの式で表せば良い。
Aは、Cの1つ前の平方数の次の数なので、
\(A=(n-1)^2+1=n^2-2n+1+1=n^2-2n+2\)
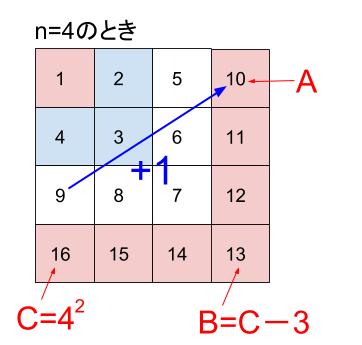
\(A=(n-1)^2 +1\)
\(B=n^2-n+1\)
\(C=n^2\)
あとは、AとBとCの和が3の倍数になることを示す。
3の倍数とは、「3×整数」なので、これを示します。
証明
\(A=n^2-2n+2\)
\(B=n^2-n+1\)
\(C= n^2\)
となる。
\(A+B+C=3n^2-3n+3=3(n^2-n+1)\)
nは2以上の整数なので、\(3(n^2-n+1)\)は3の倍数となる。
証明終了。
