問題
下の図のように、\(AB=25cm,BC=15cm,CA=20cm,AD=20cm\) の三角柱の水そうに,水位が \(15cm\) になるように水を入れました。この水そうを,長方形 \(ADEB\) が底面となるように水平な机の上におきました。このとき水位は何 \(cm\) になりますか。ただし,中の水はこぼれません。
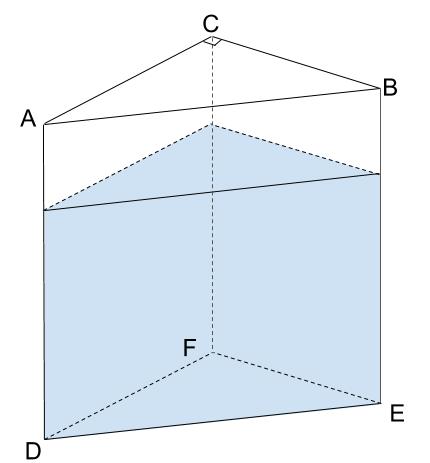
解説
高さ \(20cm\) の水そうに、水位が \(15cm\) なので、
水は三角柱の容器全体の \(\displaystyle \frac{3}{4}\) 入ってて、
空気は三角柱の容器全体の \(\displaystyle \frac{1}{4}\) です。
そして、傾けたときの様子を図示すると、
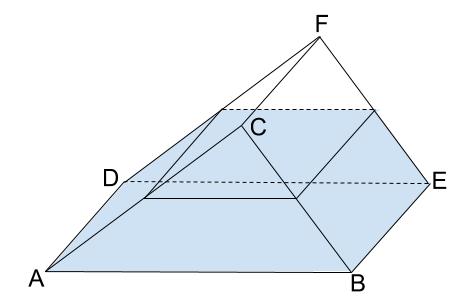
空気の部分は、三角柱ですね。
この空気部分(三角柱)と容器全体(三角柱)は、
どちらも高さが \(CF\) であり、
\(2\) つは高さの等しい三角柱です。
この空気部分は容器全体の \(\displaystyle \frac{1}{4}\) なので、
空気部分の底面積が、容器全体の底面積の \(\displaystyle \frac{1}{4}\) になっています。
底面積だけに注目しましょう。
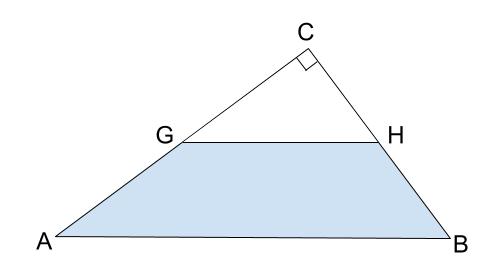
容器の底面は、三角形 \(CAB\)
空気部分の底面は、三角形 \(CGH\)
三角形 \(CAB\) と三角形 \(CGH\) は相似です。
いわゆるピラミッド型相似ですね。
相似な図形の面積の比が \(4:1\) なので
つまり相似比が \(2:1\) です。
※面積比が \(2^2:1^2\) だから。
さて、求める目標は
このときの水位です。
下図の\(QP\) の長さが目標です。
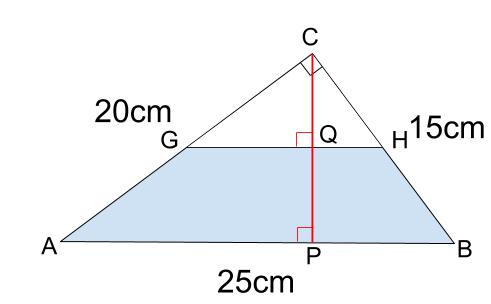
相似比が \(2:1\) ですから、\(CP:CQ=2:1\) なので、\(QP\) の長さは \(CP\) の長さの \(\displaystyle \frac{1}{2}\) となります。
\(CP\) の長さは、相似からでも面積からでも出せるようになっておきましょう。
\(CP=12cm\) ですね。
より求める長さ \(QP=6cm\)
と求まります。
スポンサーリンク
