問題
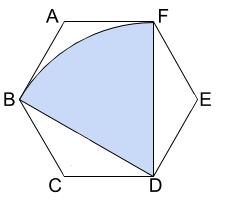
下の図で、六角形 \(A,B,C,D,E,F\) は \(1\) 辺の長さが \(2cm\) の正六角形である。
この六角形の対角線 \(DB\) を半径とし、角 \(BDF\) を中心角とするおうぎ形 \(DBF\)
の面積を求めなさい。ただし、円周率を \(\pi\) とする。
解説
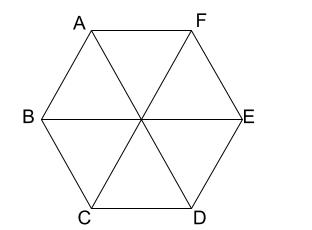
正六角形の重要性質ですが、下図のように
合同な正三角形 \(6\) つに分割されます。
本問は、 \(1\) 辺の長さが \(2cm\) の正六角形なので
正三角形の \(1\) 辺の長さも \(2cm\) です。
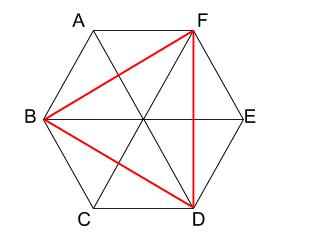
この正三角形の高さは \(\sqrt{3}cm\) なので、
\(FD=\sqrt{3}×2=2\sqrt{3}(cm)\)
つまり、おうぎ形 \(DBF\) の半径の長さは、\(2\sqrt{3}cm\) です。
また、三角形 \(BDF\) は正三角形なので、
おうぎ形 \(DBF\) の中心角である角\(BDF\) は \(60°\) です。
よって、半径 \(2\sqrt{3}cm\) 中心角 \(60°\) のおうぎ形の面積は
\( (2\sqrt{3})^2 \pi ×\displaystyle \frac{60}{360}=2 \pi (cm^2)\)
と求まりました。
スポンサーリンク
