問題
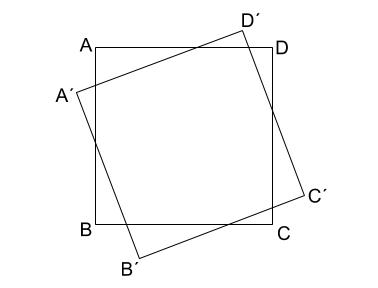
下の図は正方形 \(ABCD\) を、ある点 \(O\) を中心に回転させた図です。
回転させたのち、 \(A\) が移動した点が \(A´\)、 \(B\) が移動した点が \(B´\)、
\(C\) が移動した点が \(C´\)、 \(D\) が移動した点が \(D´\) です。
回転の中心 \(O\) の位置を定規とコンパスを用いて作図しなさい。
解説
とても難しい問題ですが、
回転の中心を定めるということですから・・・
まずはラフスケッチです。
正しい位置はとれませんが、
だいたいこんな感じ、という下書きが重要です。
\(OBB´\) はおうぎ形です。
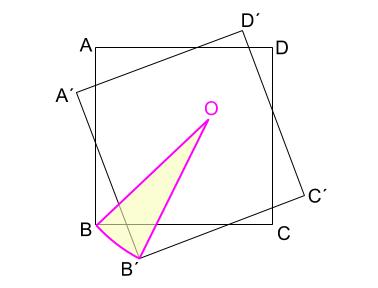
\(OCC´\) はおうぎ形です。
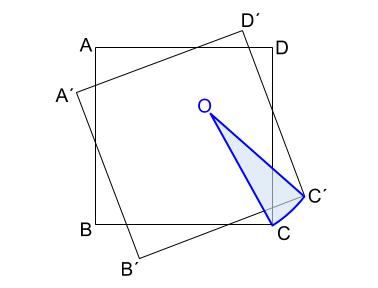
これで、作図方法がピンときた人もいるでしょう。
\(2\) つのおうぎ形、
\(OBB´\) と \(OCC´\) の中心は同じ \(O\) なのですから・・・
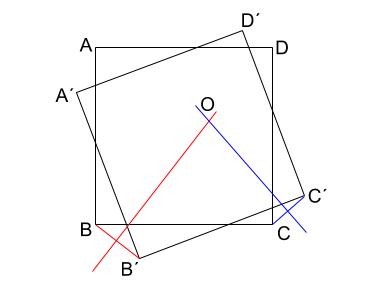
\(BB´\) の垂直二等分線上に、 \(O\) はある。
かつ、
\(CC´\) の垂直二等分線上に、 \(O\) はある。
よって、
\(2\) つの垂直二等分線をひき、その交点が \(O\) です。
このページでは垂直二等分線の作図は、すでに知っているものとします。
抜けている人は中学1年の作図のページを読みましょう。
※もちろん \(AA´\) や \(DD´\) の垂直二等分線も \(O\) を通りますので、
そちらからの作図も可能です。
スポンサーリンク
