問題
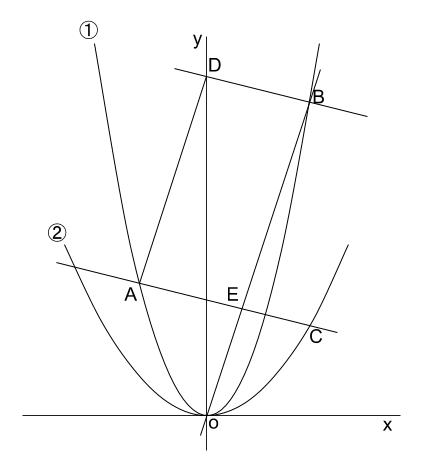
下図において、①は関数 \(y=ax^2 (a \gt \displaystyle \frac{1}{3})\) のグラフであり、②は関数 \(y=\displaystyle \frac{1}{3}x^2\) のグラフである。
点 \(A\) は放物線①上の点であり、その \(x\) 座標は \(-2\) である。
また、 \(2\) 点 \(B,C\) は、それぞれ放物線①、②上の点であり、その \(x\) 座標はともに \(3\) である。
点 \(B\) を通り、直線 \(CA\) に平行な直線と \(y\) 軸との交点を \(D\) とし、
直線 \(CA\)と直線 \(OB\)との交点を \(E\) とする。四角形 \(DAEB\) が平行四辺形に
なるときの、 \(a\) の値を求めなさい。
解説
いろいろ複雑な問題です。
何はともあれ、わかっている情報を図に書き込みます。
情報整理をしないと、スタートがきれません。
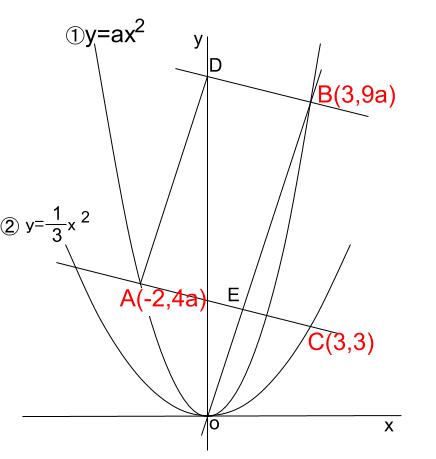
で、何をする問題だったか頭を整理しましょう。
\(a\) を求める問題です。
つまり、\(a\) の値しだいでは、問題のような図にはならないということです。
問題の図のようになる \(a\) を求めよ、ということです。
つまり、
\(D\) の \(x\) 座標が \(0\) で
\(E\) が \(OB\) 上の点で、
\(E\) が \(AC\) 上の点で、
四角形 \(DAEB\) が平行四辺形になる。
そんな \(a\) です。
たくさんの条件があるので、どこから攻めるかで何通りかの解き方があります。
例えば、点 \(E\) の座標を \(a\) を用いて表現できます。
その手順は、
直線 \(OB\) の式を求め、
直線 \(AC\) の式を求め、
それらを連立すれば、点 \(E\) の座標が\(a\) を用いて表現できます。
その後は\(AE\) と \(DB\) が平行で、長さが等しいときの \(D\) の座標が\(a\) を用いて表現できます。
その \(D\) の \(x\) 座標が \(0\) になるような \(a\) が求める値です。
ちなみにこの解法はまったくオススメできません。
もの凄く計算が面倒なのです。
はっきり言って、とてもじゃないけどやってられません。
別の条件から攻めたほうがよいです。
平行四辺形になるとき成り立つことを調べる
\(D\) の \(x\) 座標が \(0\) で、
\(DAEB\) が平行四辺形になるという条件から攻めてみましょう。
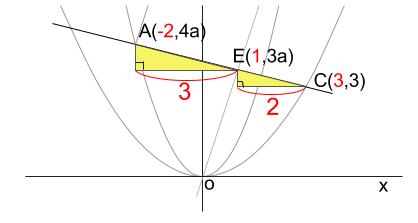
このとき、下図の三角形が合同になります。
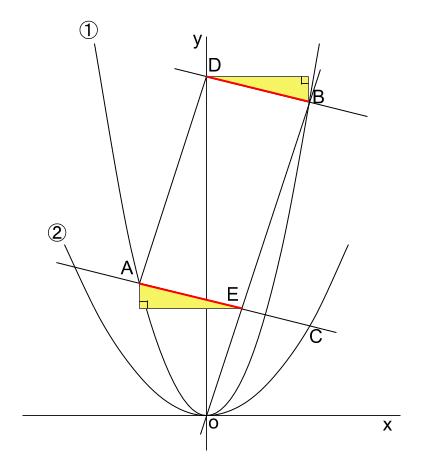
\(D\) の \(x\) 座標が \(0\) なので、
\(B\) の \(x\) 座標より、黄色い直角三角形の横の長さは \(3\) です。
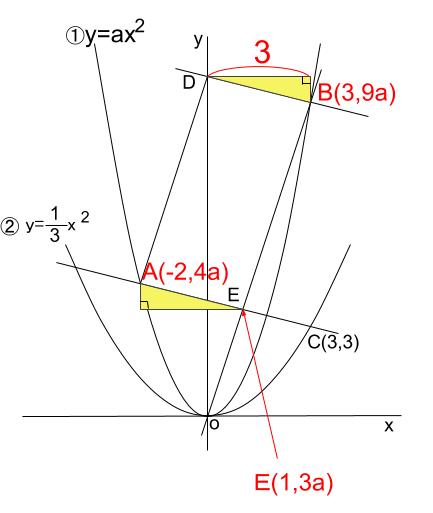
すると、\(E\) の \(x\) 座標は \(-2+3=1\) とわかります。
また、
\(OB\) を通る直線の式が \(y=3ax\) なので、
\(E\) の \(y\) 座標は \(3a\) とわかります。
※\(E\) は \(OB\) 上の点だからです。
さて、次です。
残った点 \(D\) に目が行ってしまいますが、
実はそこを探っても答えは出てきません。
黄色い三角形の高さは 点 \(A,E\) の \(y\) 座標の差より \(a\) であり、
これを用いると \(D(0,10a)\) とわかります。
しかしこれ以上先には進みません。
まだ使っていない情報がありますね。
それは、
\(A,E,C\) が一直線上にある、
ということなのです。
\(A,E,C\) すべての座標がわかっているので、あとは計算するのみですね。
まず、\(A,E\) を通る直線の式を求めます。
点 \(C\) がその直線上にのるような \(a\) が求める答えとなります。
このようにガツガツ計算で解くこともできますが、
今回はさらに図形的性質を用いて解き進めてみましょう。
※計算による解法は後述します。
※ \(AE\) の傾きと \(EC\) の傾きが等しい、という式でも解けます。
図形的に解く
さて、 \(A,E,C\) が一直線上にあるならば、下図の \(2\) つの黄色い三角形は相似になります。
各点の \(x\) 座標から、黄色い三角形の横の長さは \(3\) と \(2\)
よって、相似比は \(3:2\) です。
※もはや \(2\) つの放物線などいりません。
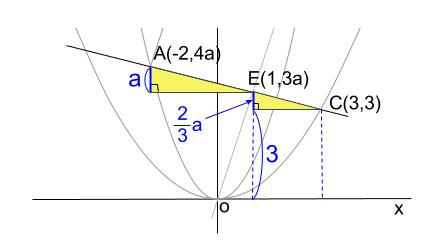
よって、高さの比も \(3:2\) なので、
小さい方の黄色い三角形の高さは
\(a×\displaystyle \frac{2}{3}=\displaystyle \frac{2}{3}a\)
よって、\(C,E\) の \(y\) 座標より、
\(3+\displaystyle \frac{2}{3}a=3a\)
これを解いて
\(a=\displaystyle \frac{9}{7}\)
これで求まりました。
別解・ガツガツ計算で解く
\(A,E,\) を通る直線の式を求め、点 \(C\) がその上にある、という解法です。
\(A\) から \(E\) まで
\(x\) の増加量は \(1-(-2)=3\)
\(y\) の増加量は \(3a-(4a)=-a\)
よって、\(A,E\) を通る直線の傾きは
\(傾き=\displaystyle \frac{-a}{3}\)
\(A,E\) を通る直線の切片を \(P\) とすれば、
\(A,E\) を通る直線の式は
\(y=\displaystyle \frac{-a}{3}x+P\)
この式に点 \(E\) の座標を代入して計算すれば、
\(P=\displaystyle \frac{10a}{3}\) と求まり、
\(A,E\) を通る直線の式は
\(y=\displaystyle \frac{-a}{3}x+\displaystyle \frac{10a}{3}\)
です。
先ほど求めた直線上に点 \(C\) があるような \(a\) を求めたいので、
直線の式に、\(C\) の座標 \((3,3)\) を代入すると、
\(3=\displaystyle \frac{-a}{3}×3+\displaystyle \frac{10a}{3}\)
これを計算すれば、
\(a=\displaystyle \frac{9}{7}\)
これが求める答えです
スポンサーリンク
