問題
下の図のように、円周上に、 \(5\) 点 \(A,B,C,D,E\) があり、\(\stackrel{ \Large \frown }{ AB }=\stackrel{ \Large \frown }{ CD }\) である。
また、線分 \(CE\) と線分 \(BD\) の交点を \(F\) 、線分 \(CE\) と線分 \(AD\) の交点を \(G\) とし、線分 \(DE\) 上に \(BD /\!/ GH\) となる点 \(H\) とる。
次の問いに答えなさい。
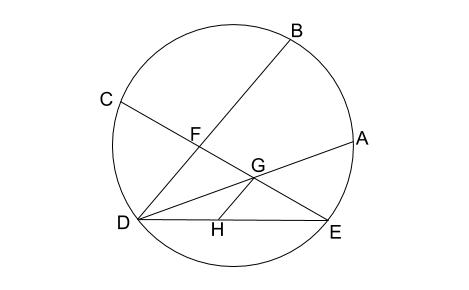
(1)\(\triangle DEG \backsim \triangle DGH\) となることを証明しなさい。
(2)\(EG=GF,GH=3cm\) のとき、線分 \(EG\) の長さを求めなさい。
解説
(1)\(\triangle DEG \backsim \triangle DGH\)
明らかに、「\(2\) つの角が等しい」から相似を示すしかありません。
目標の \(2\) つの三角形から、どこの角が等しいと言えそうか見てみます。
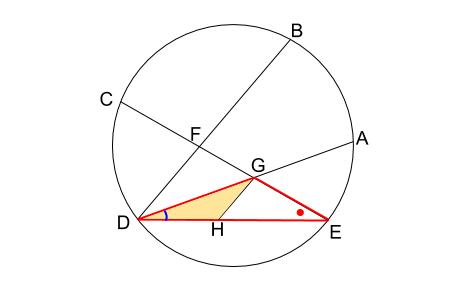
青い角は「共通なので」等しいです。
あと \(1\) つです。
このような問題では、円周角に着目するしかありません。
赤丸の角が \(\stackrel{ \Large \frown }{ CD }\) の円周角なので、
きっとこれを利用することになると予想しましょう。
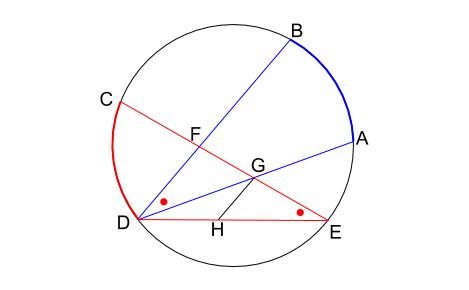
さらに問題文で、\(\stackrel{ \Large \frown }{ AB }=\stackrel{ \Large \frown }{ CD }\)
と与えられているので、\(\stackrel{ \Large \frown }{ CD }\) の円周角を利用することも明らかでしょう。
\(\stackrel{ \Large \frown }{ AB }\) の円周角と,
\(\stackrel{ \Large \frown }{ CD }\) の円周角は等しいので、下図の赤丸は等しくなります。
さらに、 \(BD /\!/ GH\) なので、平行線の錯角は等しく下図のようになります。
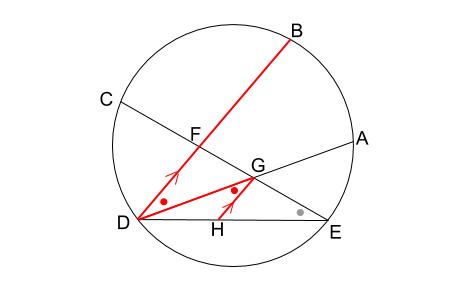
これで、\(\triangle DEG\) と \(\triangle DGH\) の \(2\) つの角が等しいことがいえます。
あとはこれを文章にまとめます。
証明の文は、基本なので省略します。
(2)線分 \(EG\) の長さ
\(EG=GF,GH=3cm\) という与えられた情報を図にかきこみます。
\(EG\) の長さが目標ですが・・・
この図を見て、解法が思いつくならばそれで終わりなのですが、
今回はこの図をいくら見ても解けないのではないでしょうか。
どうやって解いていいかわからないとき・・・
大事なことがあります。
中学数学において、
(1)は(2)を解くためのヒントになっていることが多い!
前の小問が、後の小問を解くための準備になっていることが良くあります。
ですので今回も、(1)で示した \(\triangle DEG \backsim \triangle DGH\)
が、(2)を解くための鍵になっている可能性があります。
\(\triangle DEG \backsim \triangle DGH\) に着目します。
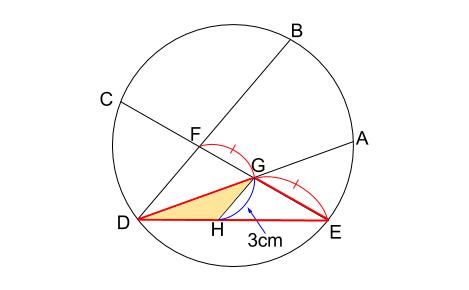
さて、\(\triangle DEG\) と \(\triangle DGH\) の相似比など、何か情報を得たいのですが、
このままでは解けません。相似比も不明です。
問題を解くためには、このままでは情報が足りません。
ここで、\(EG=GF\) という情報が、
このままではまったく \(\triangle DEG\) と \(\triangle DGH\) に関係ない情報
であることに気づきましょう。
この \(EG=GF\) という情報を、\(\triangle DEG\) と \(\triangle DGH\) に結び付けるには・・・
ピラミッド型相似に気付いてほしい問題なのでした。
平行線あれば相似あり、なのです。
よって、\(DH:HE=1:1\) がわかります。
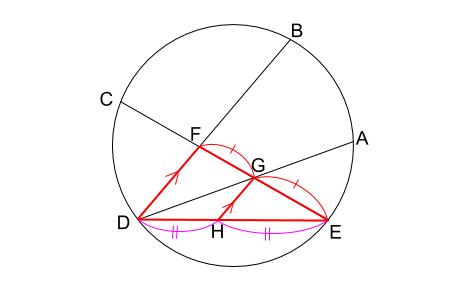
ここまで分かった情報を、
\(\triangle DEG\) と \(\triangle DGH\) の関係がわかるようにまとめましょう。
小さい方の \(\triangle DGH\) をぬき出して、ミスを減らしましょう。
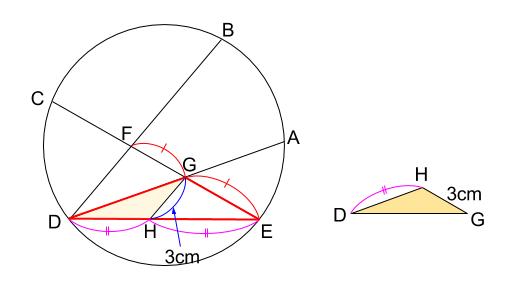
ここまでやっても、まだゴールが見えてこないです・・・
かなり難しい問題です。
分からないときは文字でおいて、立式です。
最終的に求める長さである \(EG=x\) とおいてみましょう。
またピンクの線分 \(1\) つを \(y\) とおいてみましょう。
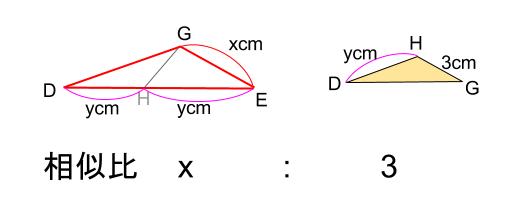
対応する線分の比が相似比なので、相似比は \(x:3\) です。
これを用いて、
\(\triangle DEG\) における \(GD\) の長さを求めます。
また、 \(\triangle DGH\) における \(DG\) の長さを求めます。
この \(2\) つは同じ辺の長さなので等しいです。
これを立式します。
\(\triangle DEG\) における \(GD\) の長さ
\(y×\displaystyle \frac{x}{3}=\displaystyle \frac{xy}{3}\)
\(\triangle DGH\) における \(DG\) の長さ
\(2y×\displaystyle \frac{3}{x}=\displaystyle \frac{6y}{x}\)
より、
\(\displaystyle \frac{xy}{3}=\displaystyle \frac{6y}{x}\)
\(x^2=18\)
\(x=\pm 3\sqrt{2}\)
\(x\) は \(0\) より大きいので、
\(x= 3\sqrt{2}\)
これが求める長さです。
別解
(1)で証明した、\(\triangle DEG \backsim \triangle DGH\) とは、
別の三角形の相似に気づければ、計算はかなり楽になります。
下図の緑と水色の三角形の相似です。もちろん \(2\) つの角から相似とわかります。
青丸の角は、平行線の同位角です。
\(FD=6cm\) は、ピラミッド相似からわかります。
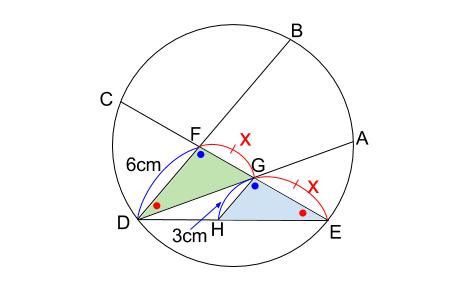
対応する辺の比は等しいので、
\(6:x=x:3\)
から、\(x= 3\sqrt{2}\) が得られます。
(1)で考えさせられた相似とは別のものから解く、というのはなかなか
気づきづらいものがあります。
(1)で、\(FDG\) と \(GEH\) の相似を証明させればいいのに・・・
意地悪な出題ですね。
このような出題もあり得るというのも知っておくべきなんですね。
スポンサーリンク
