問題
下の図のように、\(AB=4,AD=3,AE=2\) の直方体 \(ABCD-EFGH\) がある。
点 \(P\) は線分 \(AC\) 上の点で、 \(AP:PC=2:1\)、点 \(Q\) は線分 \(DF\) 上の点で、 \(DQ:QF=2:1\) をみたす点である。
次の問いに答えなさい。
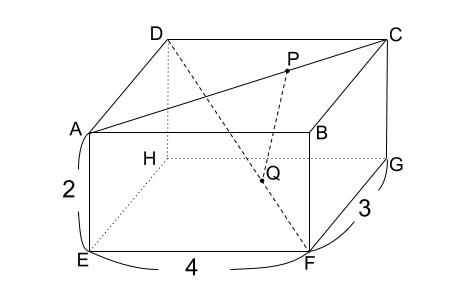
(1)\(4\) 点 \(A,B,P,Q\) を頂点とする四面体の体積を求めなさい。
(2)\(PQ\) の長さを求めなさい。
解説
難しいですが、重要なことがたくさん学べる良問です。
ゆっくり \(1\) つ \(1\) つ身につけていきましょう。
(1)\(4\) 点 \(A,B,P,Q\) を頂点とする四面体の体積
目標の四面体は、下図のようになっています。
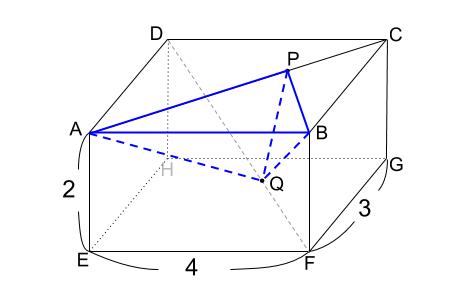
どの面を底面とし、どこを高さとすれば求められるのか考えてください。
やはり、三角形 \(ABP\) を底面とするのが良さそうですね。
そのときの高さは、 \(Q\) から \(ABP\) に引いた垂線の長さになります。
下図の \(QR\) が高さです。
つまり、
三角形 \(ABP\) の面積と、\(QR\) の長さを求めれば、体積が求まります。
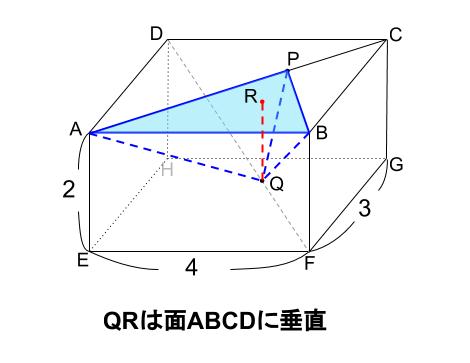
順に見ていきましょう。
三角形 \(ABP\) の面積
\(AP:PC=2:1\) なので、
点 \(P\) は 下図のような位置にあります。
三角形 \(ABC\) と \(AIP\) がピラミッド型相似になっています。
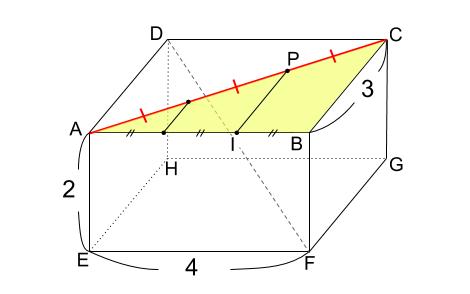
よって
\(PI=2\) なので、三角形 \(ABP\) の面積は
\(4×2× \displaystyle \frac{1}{2}=4\)
と求まります。
※比を用いて求めてもかまいません。
\(QR\) の長さ
\(DQ:QF=2:1\) なので、
点 \(Q\) は 下図のような位置にあります。
三角形 \(DHF\) と \(QJF\) がピラミッド型相似になっています。
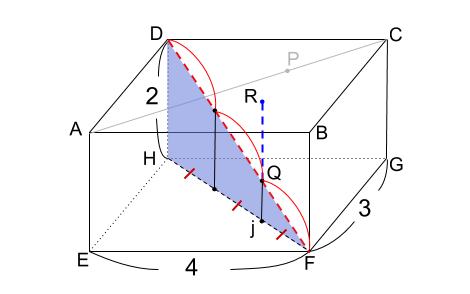
よって
\(QJ=2× \displaystyle \frac{1}{3}= \displaystyle \frac{2}{3}\) なので、
\(QR=2-\displaystyle \frac{2}{3}=\displaystyle \frac{4}{3}\) です。
以上より、
\(A,B,P,Q\) を頂点とする四面体の体積は、
底面 \(ABP\) の面積が \(4\)
高さ \(QR\) が \(\displaystyle \frac{4}{3}\) なので、
\(4×\displaystyle \frac{4}{3}×\displaystyle \frac{1}{3}=\displaystyle \frac{16}{9}\)
これが求める体積です。
(2)\(PQ\) の長さ
点 \(P,Q\) の位置を正確に把握しなくては計算ができません。
点 \(Q\) の位置について、下図のように
三角形 \(HEF\) と三角形 \(JKF\) のピラミッド型相似にも着目しましょう。
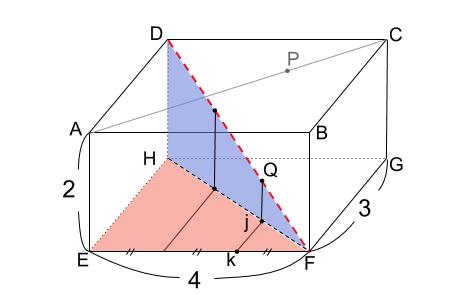
つまり、点 \(P\) と 点 \(Q\) は、下図のような平面上の点です。
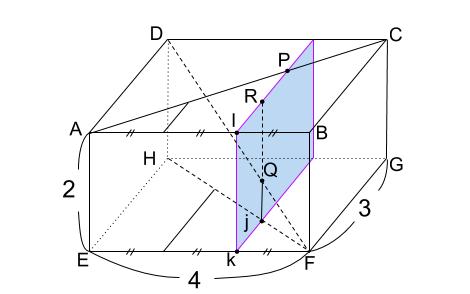
この平面をぬき出すと下図のようになっています。
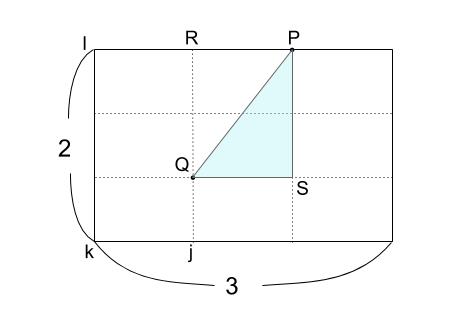
水色の直角三角形 \(PQS\) に三平方の定理を使えば良いですね。
\(QS=1,SP=\displaystyle \frac{4}{3}\) なので、
\(PQ=\displaystyle \frac{5}{3}\)
これが求める長さです。
※\(3:4:5\) に気づけば、三平方の定理も必要ありません。
スポンサーリンク
