問題
下の図は、線分 \(AB\) を直径とする半円で、点 \(C\) は\(\stackrel{ \Large \frown }{ AB }\) 上にある。\(\stackrel{ \Large \frown }{ AC }\) 上に点 \(D\) を、
\(\stackrel{ \Large \frown }{ AD }=\stackrel{ \Large \frown }{ CD }\) となるようにとり、線分 \(AC\) と線分 \(BD\) の交点を \(E\) とする。次の問いに答えなさい。
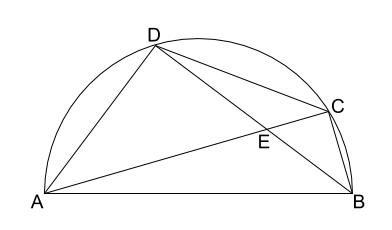
(1)\(\triangle ABE \backsim \triangle DBC\) を証明しなさい。
(2)\(AB=10cm,AD=6cm\) のとき
①線分 \(AE\) の長さを求めなさい。
②線分 \(BC\) の長さを求めなさい。
解説
(1)三角形 \(ABE\) と三角形 \(DBC\) が相似
もちろん、角度から相似がいえます。
円周角の定理より、等しい角があり、そして「相似」
これが非常に多い定番です。
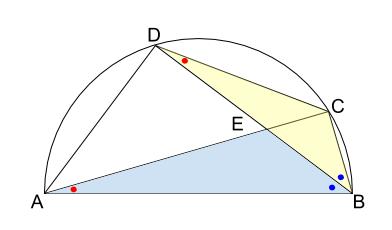
赤丸の角は、\(\stackrel{ \Large \frown }{ BC }\) の円周角。
青丸の角は、\(\stackrel{ \Large \frown }{AD }\) と \(\stackrel{ \Large \frown }{ CD }\) の円周角。
\(2\) つの角が等しいので、相似です。
証明の解答例は省略します。
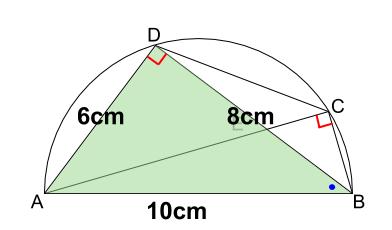
(2)\(AB=10cm,AD=6cm\) のとき \(AE,BC\) の長さ
様々な情報が隠れています。
まず、直径があるので、半円の円周角 \(90°\) です。
下図の赤い直角です。
そして、直角三角形 \(DAB\) が \(3:4:5\) の有名三角形です。
\(BD=8cm\) です。
次に、直角三角形 \(DEA\) と直角三角形 \(CEB\) が
直角三角形 \(DAB\) と相似です。
直角と青丸の角の大きさからわかります。
よって、直角三角形 \(DEA\) と直角三角形 \(CEB\) も
辺の比が \(3:4:5\) の有名三角形です。
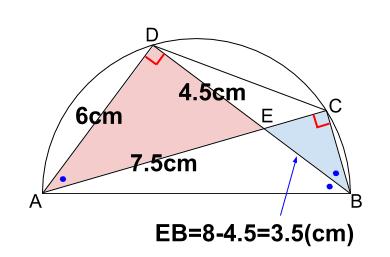
よって、\(AE=7.5(cm),DE=4.5(cm)\)
\(BE=BD-DE\) なので、
\(BE=8-4.5=3.5\)
\(BE:CB=5:4\) なので、
\(CB=3.5×\displaystyle \frac{4}{5}=2.8(cm)\)
以上より、\(AE=7.5cm,BC=2.8cm\)です。
スポンサーリンク
