問題
下の図のように、円 \(O\) の周上に、点 \(A,B,C\) がある。
\(\angle BAC\) の二等分線と線分 \(BC\) 、円 \(O\) との交点をそれぞれ \(D,E\) とする。
次の問いに答えなさい。
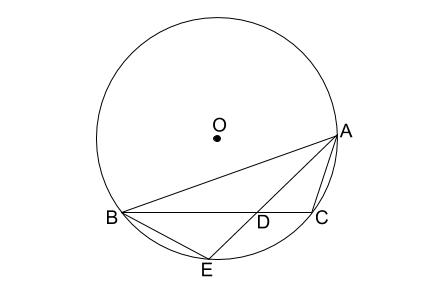
(1)\(\triangle ABE \backsim \triangle BDE\) となることを証明しなさい。
(2)\(AB=12cm,BD=8cm,BE=6cm\) とするとき、線分 \(AD\) の長さを求めなさい。
解説
(1)\(\triangle ABE \backsim \triangle BDE\)
明らかに、「\(2\) つの角が等しい」から相似を示すしかありません。
また、明らかに円周角に着目するしかありません。
\(\stackrel{ \Large \frown }{ EC }\) の円周角より、赤丸の角が等しく、
また、\(AE\) は \(\angle BAC\) の二等分線なので \(\angle BAE\) も赤丸です。
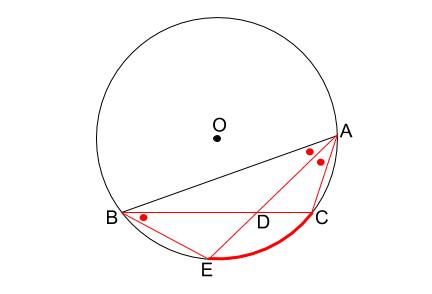
ここで、\(\triangle ABE\) と \(\triangle BDE\) に着目すれば
赤丸の角と、青い角(共通なので)の \(2\) つの角が等しいので、相似がいえます。
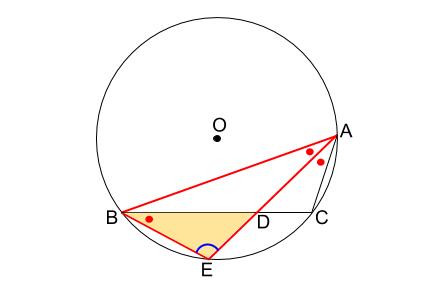
あとはこれを文章にまとめるだけです。
最終的な解答は省略します。
(2)線分 \(AD\) の長さ
\(AB=12cm,BD=8cm,BE=6cm\) という与えられた情報を図にかきこみます。
青い線分の長さを求めることが目標です。
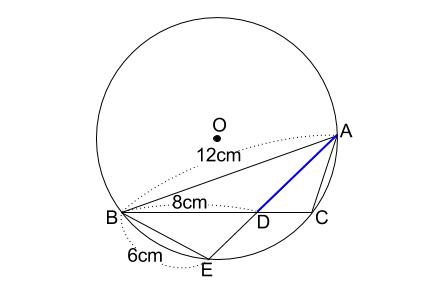
この図を見て、解法が思いつくならばそれで終わりなのですが、
今回はこの図をいくら見ても解けないのではないでしょうか。
どうやって解いていいかわからないとき・・・
大事なことがあります。
中学数学において、
(1)は(2)を解くためのヒントになっていることが多い!
前の小問が、後の小問を解くための準備になっていることが良くあります。
ですので今回も、(1)で示した \(\triangle ABE \backsim \triangle BDE\)
が、(2)を解くための鍵になっている可能性があります。
\(\triangle ABE \backsim \triangle BDE\) に着目します。
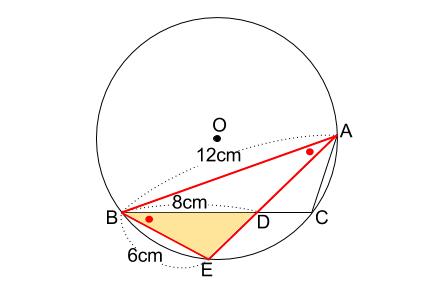
どちらの三角形も、 \(2\) 辺の長さがわかっています。
これは相似比を使ってなんとかなりそうです。
ミスを減らすためにも、小さいほう \(\triangle BDE\) を、 \(\triangle ABE\)
と同じ向きにぬき出しましょう。
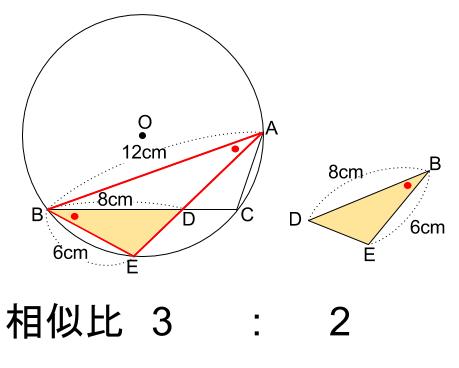
相似比は \(AB:BD=12:8=3:2\) です。
よって
\(EA=EB×\displaystyle \frac{3}{2}=6×\displaystyle \frac{3}{2}=9(cm)\)
\(DE=BE×\displaystyle \frac{2}{3}=6×\displaystyle \frac{2}{3}=4(cm)\)
以上より、
\(AD=EA-DE=9-4=5(cm)\)
これで求まりました。
スポンサーリンク
