問題
下の図で、①は関数 \(y=-\displaystyle \frac{1}{4}x^2\) のグラフである。
点 \(A,B\) は①上にあり、点 \(A\) の \(x\) 座標は \(-8\) 、点 \(B\) の \(x\) 座標は \(4\) である。②は, \(A,B\) を通る直線と \(y\) 軸との交点を \(C\) とする。
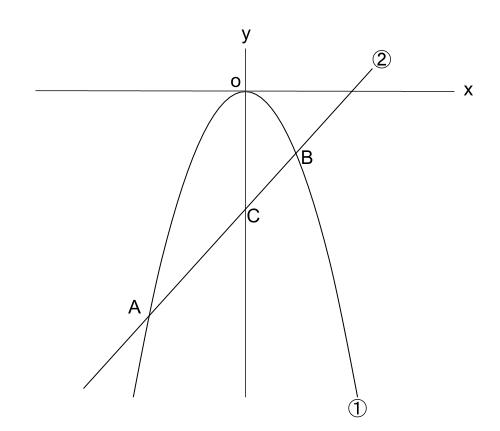
(1)\(A\) の \(y\) 座標を求めなさい。
(2)直線②の式を求めなさい。
(3)三角形 \(OAB\) の面積を求めなさい。
(4)点 \(Q\) を三角形 \(OAB\) の辺上にとり、線分 \(CQ\) が三角形 \(OAB\) の面積を二等分するとき、点 \(Q\) の座標を求めなさい。
解説
(1)から(3)は、中学3年、2乗に比例 でマスターしておかないといけない
基本問題です。
(4)が応用問題です。
(1)\(A\) の \(y\) 座標
\(y=-\displaystyle \frac{1}{4}x^2\) に \(x=4\) を代入するだけです。
\(A\) の \(y\) 座標は \(-16\) です。
わかった情報はどんどん図に書きこんでいきます。
次の問題を解くための鍵になり得るからです。
(2)直線②の式
同様に、\(B\) の \(y\) 座標は \(-4\) です。
よって、\(A(-8,-16)\) と \(B(4,-4)\) を通る直線の式です。
求め方は大丈夫ですね?
求める直線の式は、
\(y=x-8\) です。
(3)三角形 \(OAB\) の面積
\(C\) の \(y\) 座標は、\(y=x-8\) の切片より、 \(-8\) です。
より \(OC=8\) を底辺とする \(2\) つの三角形の面積の和です。
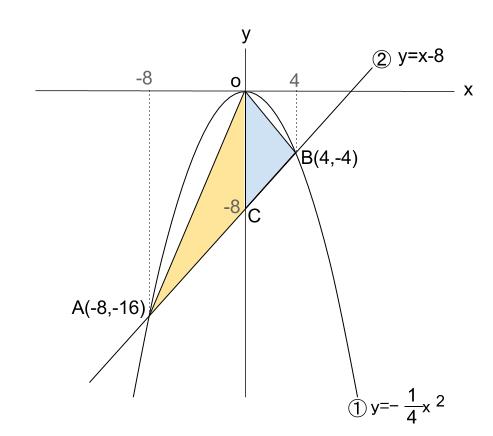
左は、 \(8×8×\displaystyle \frac{1}{2}=32\)
右は、\(8×4×\displaystyle \frac{1}{2}=16\)
合計 \(32+16=48\)
これが三角形 \(OAB\) の面積です。
単位\(cm^2\) は不必要です。
座標平面の \(1\) 目盛りの長さが与えられていないときは、
単位なしで、面積とします。
(4)三角形 \(OAB\) の面積を二等分
点 \(Q\) を三角形 \(OAB\) の辺上にとり、線分 \(CQ\) が三角形 \(OAB\) の面積を二等分するときの点 \(Q\) の座標を求める問題です。
三角形 \(OAB\) の面積を二等分なので、面積は \(24\) ずつです。
よって、点 \(Q\) は辺 \(OA\) 上で、
三角形 \(OAC\) を、 \(24\) と \(8\) に分ける 下図のようになるときです。
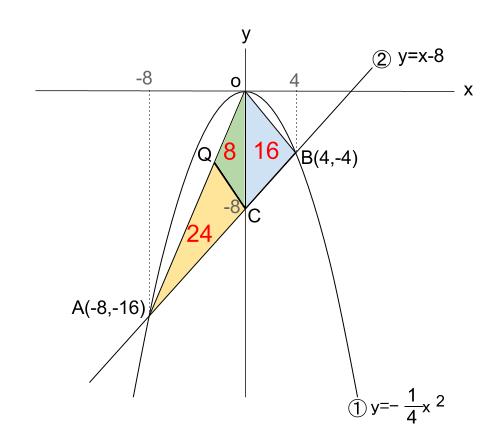
\(\triangle OQC\) の底辺を \(OC=8\) とみれば
その高さは \(2\) となるので、
点 \(Q\) の \(x\) 座標が \(-2\) と求まります。
\(O\) と \(A\) を通る直線の式は \(y=2x\) と簡単に求まるので、
点 \(Q\) の座標は \((t,2t)\) とおけます。
点 \(Q\) の \(x\) 座標、\(-2\) を \((t,2t)\) に代入して、
\((-2,-4)\) と求まります。
スポンサーリンク
