問題
下の図の線分 \(AB\) を、 \(1:2\) の比に分ける点 \(P\) を作図しなさい。

解説
有名な作図です。
何も知らない状態で、この作図方法を思いつくのは至難です。
解説を読んで理解・暗記しましょう。
ずばり、作図方針は「相似の利用」です。
ピラミッド型の三角形を利用します。
下図のような図が目標です。

どうやって作図するのかは、後の話です。
今は、\(P\) が、\(AB\) を \(1:2\) に分けていることを理解しましょう。
では作図方法です。
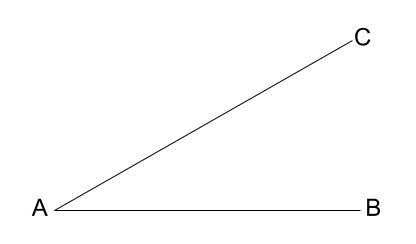
まず、線分 \(AC\) をひきます。
\(C\) はどこであってもかまいませんが
下図くらいが、後の作図がやりやすいです。
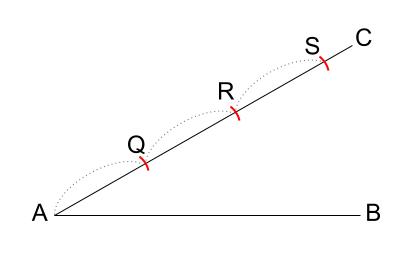
次に、コンパスを用いて、線分 \(AC\) 上に
等しい長さを \(3\) つとります。
下の図で、\(AQ=QR=RS\) です。
\(AQ\) の長さも、どれくらいであってもかまいません。
\(3\) つの長さが等しいことが重要で、その長さはいくつであってもOKです。
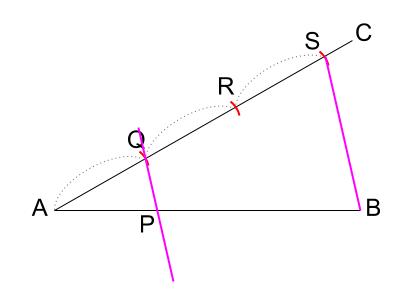
\(S\) と \(B\) を結びます。
この \(SB\) と平行で \(Q\) を通る平行線を引けば作図完了です。
\(AB\) との交点が点 \(P\) の位置です。
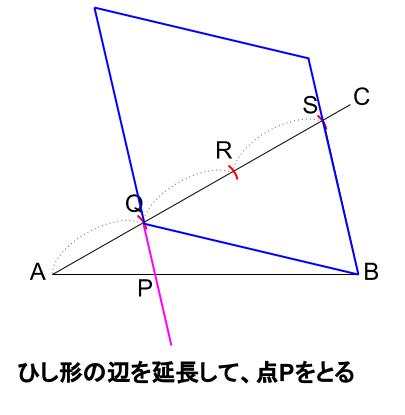
※平行線の作図は、ひし形の作図です。
\(BS\) を上に延長、
\(BQ\) を半径とする円を用いて、
\(BQ\) を \(1\) 辺とするひし形を作図することで、
平行線の作図ができます。
スポンサーリンク
