問題
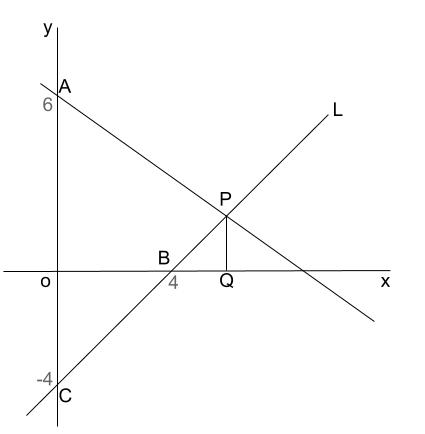
下の図で、点 \(A\) の座標は \((0,6)\) であり、直線 \(L\) は一次関数 \(y=x-4\) のグラフである。
点 \(B,C\) は直線 \(L\) 上にあり、点 \(B\) の座標は \((4,0)\)、点 \(C\) の座標は \((0,-4)\) である。
直線 \(L\) 上に点 \(P\) を、 \(x\) 座標が \(4\) より大きい数であるようにとり、点 \(P\) を通り \(y\) 軸と平行な直線を引き、 \(x\) 軸との交点を \(Q\) とします。
三角形 \(ACP\) の面積が、三角形 \(BQP\) の面積の \(5\) 倍となるとき、点 \(P\) の座標を求めなさい。
解説
まず問題の意味をしっかりと掴みましょう。
点 \(P\) がどこにあるのか、が話題です。
点 \(P,Q\) 以外のあらゆるものは固定されています。
点 \(P\) が動けば、点 \(Q\) や、直線 \(AP\) も動きます。
三角形 \(ACP\) の面積や、三角形 \(BQP\) の面積も
それに応じて変化します。
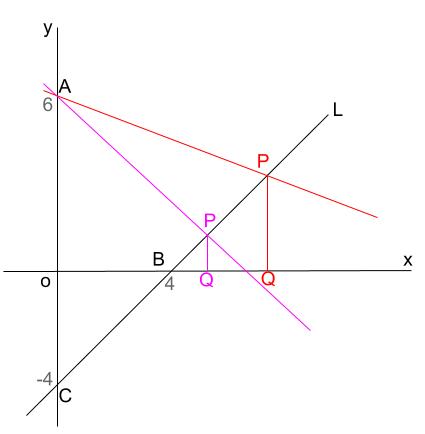
どこで、三角形 \(ACP\) の面積が、三角形 \(BQP\) の面積の \(5\) 倍となるか
という問題です。
求めたいものを文字でおき、等式をたてる。
あとは方程式を解く。
これが中学数学の王道です。
点 \(P\) の \(x\) 座標を \(t\) とおいてみましょう。
すると、いろいろな値が \(t\) で表現できます。
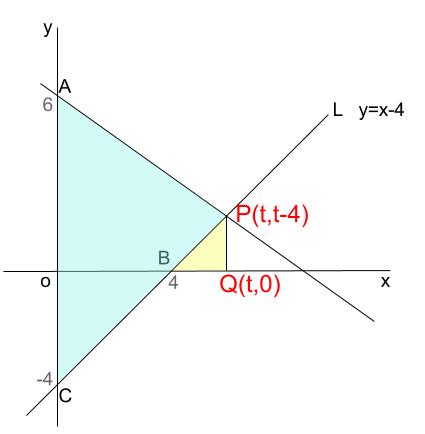
点 \(P\) は \(y=x-4\) 上の点なので、 \(y\) 座標は、 \(t-4\)
点 \(Q\) の座標は、 \((t,0)\) となります。
これを用いて、
三角形 \(ACP\) の面積も、三角形 \(BQP\) の面積も
\(t\) で表すことができます。
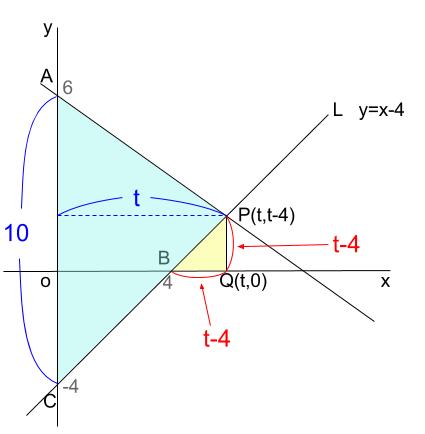
水色の三角形 \(ACP\) ですが、\(AC=10\) は \(A,C\) の \(y\) 座標から
高さ \(t\) は、点 \(P\) の \(x\) 座標からわかります。
その面積は、
\(10× t×\displaystyle \frac{1}{2}=5t\)・・・①
クリーム色の三角形 \(BQP\) ですが、\(BQ=t-4\) は \(B,Q\) の \(x\) 座標から
高さ \(t-4\) は、点 \(P\) の \(y\) 座標からわかります。
その面積は、
\((t-4)^2×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{2}(t-4)^2\)・・・②
※直線 \(L\) の傾きから、 三角形 \(BQP\) が直角二等辺三角形になることも
明らかです。
三角形 \(ACP\) の面積が、三角形 \(BQP\) の面積の \(5\) 倍となるとき、
①、②より、
\(5t=\displaystyle \frac{1}{2}(t-4)^2×5\)
あとはこの方程式を解きます。
両辺を \(5\) で割って
\(t=\displaystyle \frac{1}{2}(t-4)^2\)
両辺を \(2\) 倍して
\(2t=(t-4)^2\)
ここから先は省略します。
整理して因数分解すると
\((t-2)(t-8)=0\)
\(t=2,8\)
\(t\) は \(4\) より大きいので、
\(P\) の \(x\) 座標は \(8\) です。
よって \(P\) の座標は、 \((8,4)\)
と求まります。
スポンサーリンク
