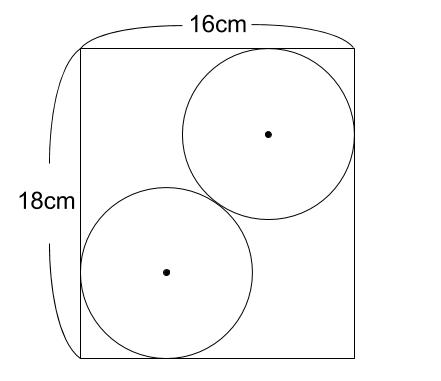
問題
下図のように、長方形の \(2\) つの辺に内接する半径の等しい \(2\) つの円があり、
円どうしも接しています。このとき、円の半径を求めなさい。
解説
求める円の半径を \(rcm\) とします。
円と接線ですから、中心と接点を結びます。
基本知識です。
そして、\(2\) つの円の中心どうしも結ぶと下図のようになります。

\(r\) を求めるためには、 \(16cm\) や \(18cm\) と結びつけるしかありません。
青い点線を延長することで、
水色の直角三角形が内部に見えてきます。
これに三平方の定理を用います。
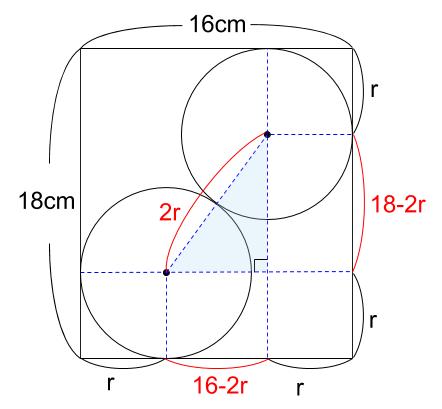
計算を楽にするために、\(3\) 辺をすべて \(2\) で割りましょう。
\(\displaystyle \frac{1}{2}\) 倍の相似な図形で計算します。
\((8-r)^2+(9-r)^2=r^2\)
\(64-16r+r^2+81-18r+r^2=r^2\)
\(145-34r+r^2=0\)
この \(2\) 次方程式は、幸いなことに簡単に因数分解できます。
\((r-5)(r-29)=0\)
\(r=5,29\)
\(r\) は明らかに長方形の辺の長さより小さいので、
題意に合う \(r\) は \(5\)
よって、
求める円の半径は\(5cm\) です。
スポンサーリンク
