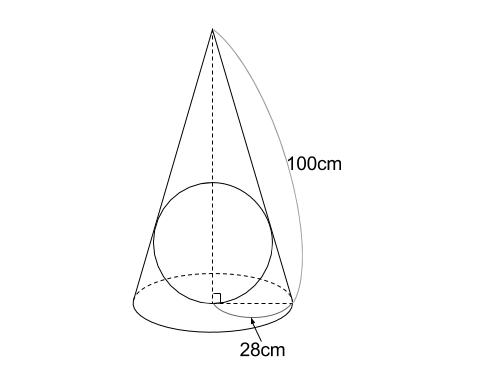
問題
下の図のように、底面の半径が \(28cm\),母線の長さが \(100cm\) の円錐に
球が内接しています。この球の半径を求めなさい。
解説
平面における、「三角形と内接円の関係」とほぼ同じです。
空間図形においても、着目すべき「平面」で解きます。
どの平面に着目すべきか考えましょう。
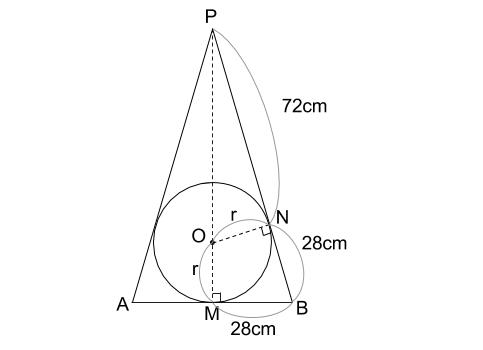
もちろん下の図のような、三角形 \(PAB\) に着目します。
\(AB\) は底面の円の直径で、底面の円の中心が \(M\) です。

三角形 \(PAB\) をぬき出します。
この平面上、さらに、線分 \(PM\) 上に球の中心 \(O\) があります。
対称性から明らかですね。
この平面で、球は切られますが、その切断面は
中心 \(O\) を含む円になります。
そして、円と接線があれば、中心と接点を結ぶのが必須知識です。
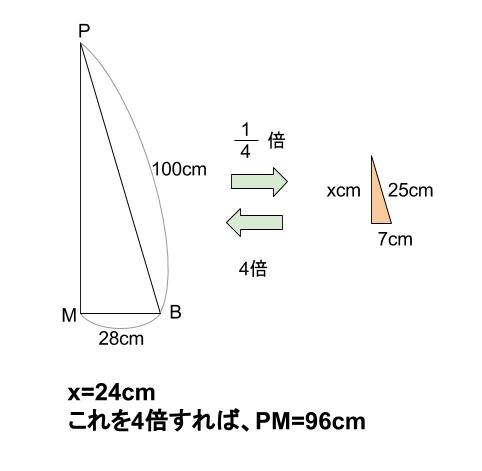
他にわかることは、三角形 \(PBM\) に三平方の定理を用いて
\(PM\) の長さを求めることです。
\(PB:BM=100:28=25:7\)
なので、
\(\displaystyle \frac{1}{4}\) 倍に縮小した直角三角形で計算すると、
\(x^2+7^2=25^2\)
\(x\) は \(0\) より大きいので、
\(x=24\)
と求まります。
つまり、\(PM=24×4=96\) です。
ここから先は、\(2\) 通りの解き方があります。
「相似」か「三平方の定理」です。
「相似」が圧倒的に楽なので、そちらを使いましょう。
三角形 \(PMB\) と三角形 \(PNO\) が相似です。
三角形 \(PNO\) を三角形 \(PMB\) と同じ向きにぬきだして考えましょう。
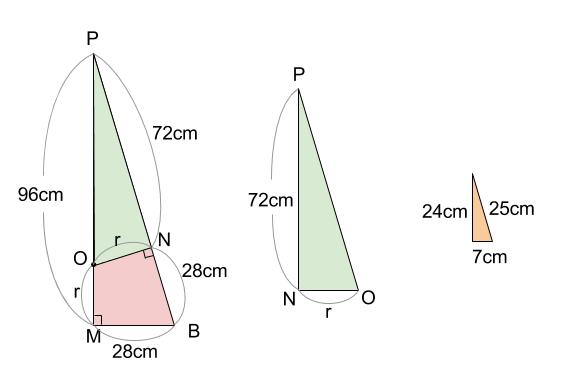
この\(2\) つの三角形は相似であり、直角をはさむ \(2\) 辺の辺の比が
\(24:7\) です。
※相似比ではないですよ!
よって\(r=NO=72×\displaystyle \frac{7}{24}=21(cm)\)
これが求める内接円の半径です。
ちなみに、
\(PO=96-21=75\)
ですが、三角形 \(PNO\) の辺の比が \(25:24:7\) であることと一致します。
矛盾なしです。
※三角形 \(PMB\) と三角形 \(PNO\) が相似で相似比が \(96:72=4:3\) からも、もちろん解けます。
\(r=NO=28×\displaystyle \frac{3}{4}=21(cm)\)
と求まります。
スポンサーリンク
