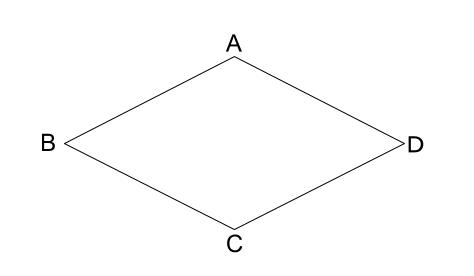
問題
下の図のひし形 \(ABCD\) の \(4\) つの辺すべてに内接する円を、
定規とコンパスを用いて作図しなさい。
解説
円の作図なので、
円の中心と、半径を定めることが目標です。
完成図をラフスケッチして、図形的性質を探りましょう。
「接している」ということは、
円の中心と接点を結ぶ半径は、接線と垂直です。
このような「暗記事項」なしに、数学パズルには挑めません。
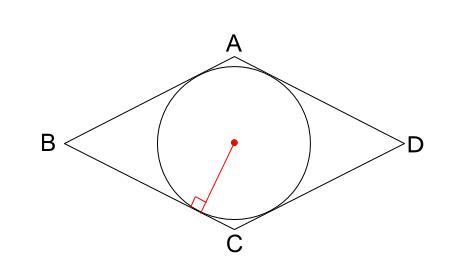
では、この円の中心はどうやって定めたらよいのでしょうか。
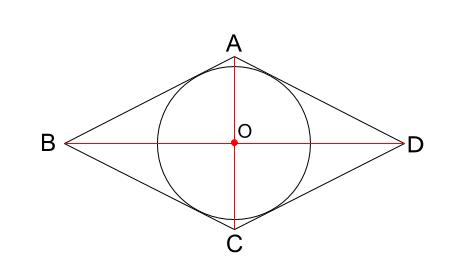
図形の対称性から、ひし形の対角線の交点であることは
直感的にわかりますね。
これで作図の方針がたちまちした。
まず
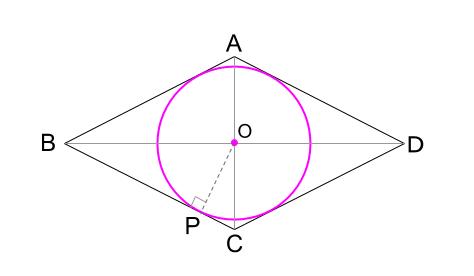
対角線を \(2\) 本ひき、交点をとります。
それが、円の中心 \(O\) です。
次に
\(O\) から、ひし形の辺のどれでもよいので、垂線を引きます。
垂線の引き方は基本中の基本なので、はここでは省略します。
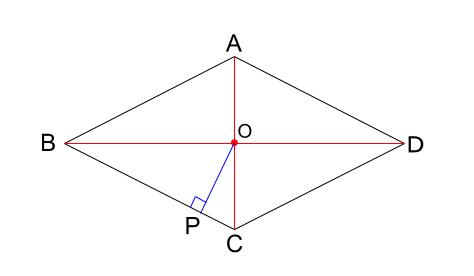
垂線と辺との交点を \(P\) とすれば、
\(OP\) を半径とする円をかけば完成です。
スポンサーリンク
