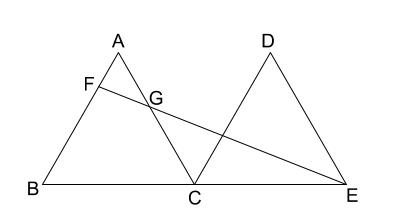
問題
下の図で、三角形 \(ABC\) と三角形 \(DCE\) はどちらも \(1\) 辺の
長さが \(4cm\) の正三角形であり、\(B,C,E\) は一直線上にある。\(AF\) の長さが \(1cm\) のとき、
\(AG\) の長さを求めなさい。
解説
平行線と相似の利用です。
あまりこのタイプの図形の練習をする機会は多くないのではないでしょうか。
確かに高校入試において、出題頻度はそれほど多くないような気がします。
しかし、準備をしておくに越したことはありません。
まず
\(AB /\!/ DC\)
です。
平行線あるところに相似ありです。
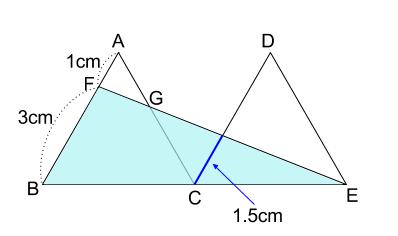
下図の水色がピラミッド型の相似で、
相似比は \(2:1\) です。
より、青い線分の長さは
\(3×\displaystyle \frac{1}{2}=1.5(cm)\) です。
また、下図のピンク色の三角形が、砂時計型相似です。
相似比は \(1:1.5=2:3\) です。
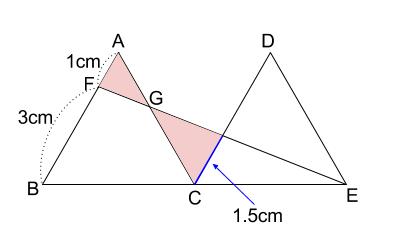
よって、 \(AG:GC=2:3\) なので、
\(AG=4×\displaystyle \frac{2}{2+3}=1.6(cm)\)
と求まります。
スポンサーリンク
