問題
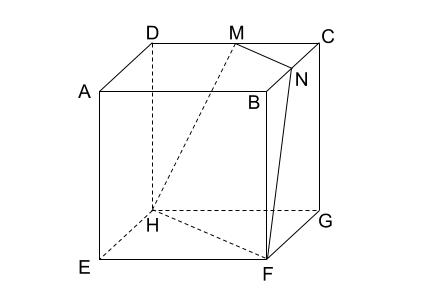
下の図のように、\(1\) 辺の長さが \(4cm\) の立方体 \(ABCD-EFGH\) がある。
辺 \(CD\) と辺 \(BC\) の中点をそれぞれ \(M,N\) とする。
線分 \(AG\) と平面 \(MHFN\) との交点を \(P\) とするとき、線分 \(AP\) の
長さを求めなさい。
解説
立体は、その一部である「平面」に着目して解きます。
\(3\) 次元のものを想像して解くのではなく、
\(2\) 次元の平面をぬき出して、紙の上で目で見て解きます。
本問ならば、\(AP\) を含む平面です。
そのような平面は無数にありますが、
もちろん、扱いやすい平面を用います。
長方形 \(AEGC\) でしょう。
\(MN\) の中点 \(Q\) と
\(HF\) の中点 \(R\) を結んだ線分上に点 \(P\) があります。
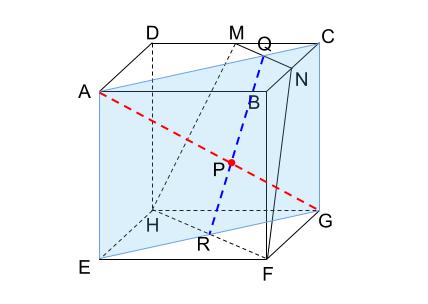
長方形 \(AEGC\) をぬき出します。
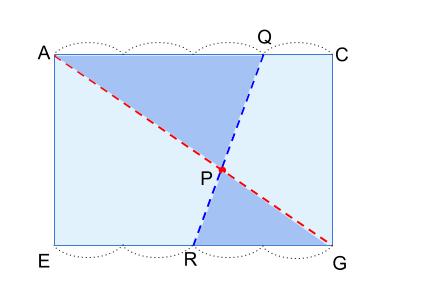
砂時計相似が見つかります。
相似比は \(AQ\) と \(GR\) の長さからわかります。
\(AQ\) は、正方形の対角線 \(4\sqrt{2}\) の \(\displaystyle \frac{3}{4}\)
\(GR\) は、正方形の対角線 \(4\sqrt{2}\) の \(\displaystyle \frac{1}{2}\)
より、相似比は \(3:2\) です。
よって、 \(AP\) の長さは、立方体の対角線 \(AG\) の \(\displaystyle \frac{3}{3+2}\) です。
\(1\) 辺が \(4cm\) の立方体の対角線の長さは \(4\sqrt{3}\) なので
\(AP=4\sqrt{3}×\displaystyle \frac{3}{3+2}=\displaystyle \frac{12\sqrt{3}}{5}\)
と求まります。
スポンサーリンク
