例題
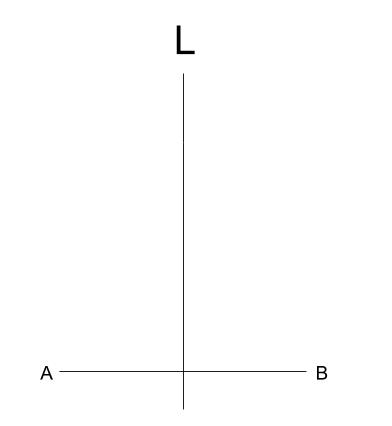
下の図のように、線分 \(AB\) とその垂直二等分線 \(L\) がある。
直線 \(L\) 上に点 \(P\) を\(\angle APB=45°\) となるようにとりたい。
このような点 \(P\) を定規とコンパスを使って作図しなさい。
解説
かなり難しい問題といえます。
どうやって作図していいか見当もつかないときは、
まずは完成図のラフスケッチからです。
※ \(45° \) が正確にとれている必要はまったくありません。
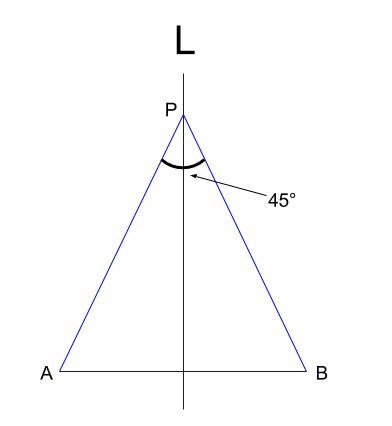
この図の図形的性質を探ることでしか、
作図の手順は見えてこないのです。
何通りか作図手順があるので、それを示します。
円周角の定理の利用
\(45°\) は \(90°\) の半分なので、以下のような円がかければ
点 \(P\) がとれます。
円周角と中心角の関係ですね。
※図はラフスケッチであり、不正確です。
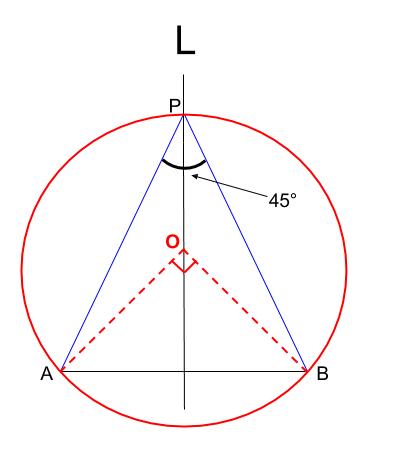
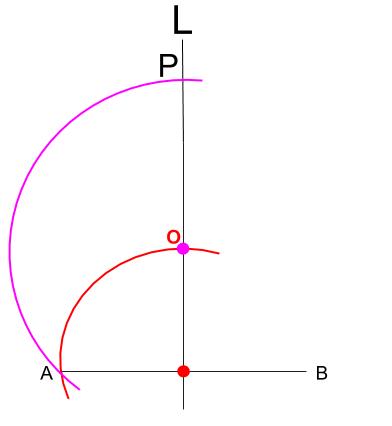
この円を目標にします。
三角形 \(OAB\) が直角二等辺三角形なので、
この円の中心 \(O\) は下図のように、\(AB\) と \(L\) の交点を中心とする円をかくことでとれます。
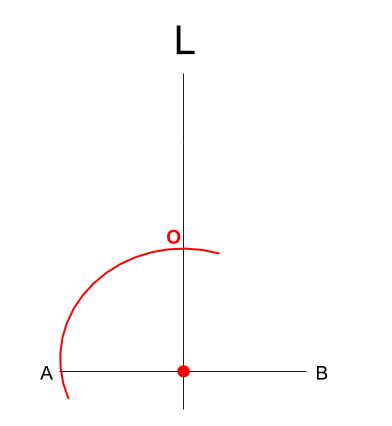
次に \(O\) を中心に半径 \(OA\) の円をかけば、点 \(P\) がとれます。
めでたしめでたし。
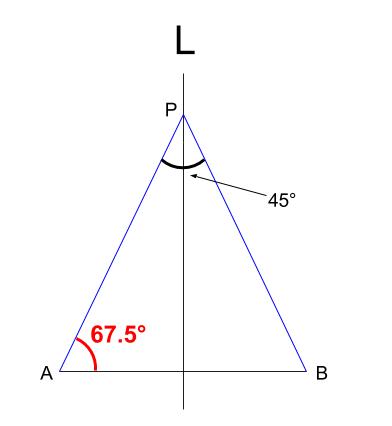
別解
下図の赤い角が \(67.5°\) です。
これは \(135°\) 二等分なので、これから作図可能です。
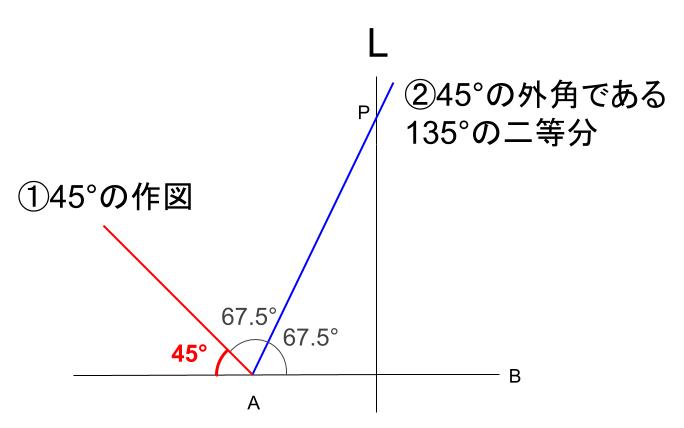
まず、\(90°\) の作図をして、それを二等分。
\(45°\) を作図します。
次に、\(45°\) の右にできた \(135°\) を二等分します。
これらの作図手順を暗記していない人は、基礎から学習しなおしましょう。
※その他の作図方法もあります。
スポンサーリンク
