問題
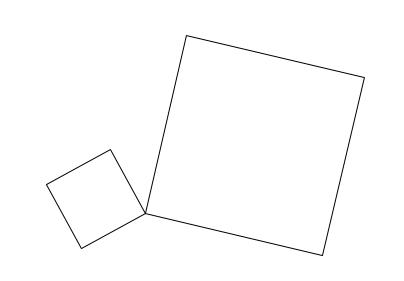
下の図のように、一辺の長さが異なる \(2\) つの正方形があり、
\(1\) つの頂点が重なっている。このとき、面積が、\(2\) つの正方形の面積の
差に等しい正方形を作図しなさい。
\(1\) つの頂点が重なっている。このとき、面積が、\(2\) つの正方形の面積の
差に等しい正方形を作図しなさい。
解答
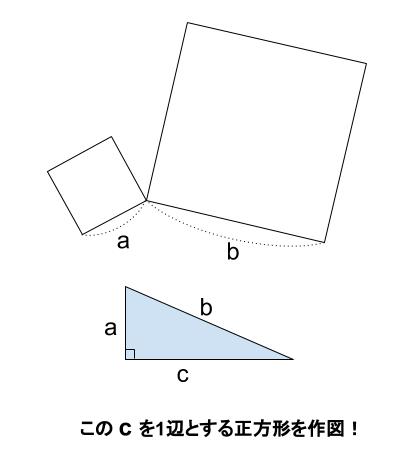
小さい方の一辺の長さを \(a\)
大きい方の一辺の長さを \(b\)
とすれば、
面積が \(b^2-a^2\) となる正方形を作図せよ、
ということです。
この式を見てピンときますね!
目標の正方形の一辺の長さが \(c\) ならば、
その面積は \(c^2\)
つまり、
\(c^2=b^2-a^2\)
どう見ても三平方の定理です。
\(a^2\) を移項すれば
\(a^2+c^2=b^2\)
これを満たすような \(c\) は、
\(b\) を斜辺、一辺を \(a\) とする直角三角形の最後の一辺です。
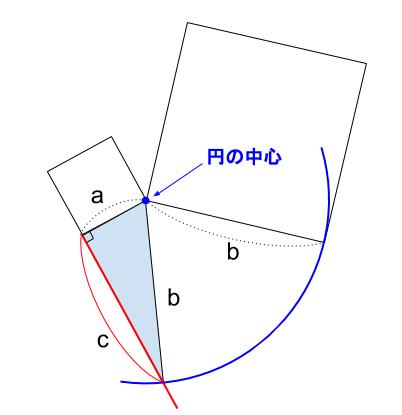
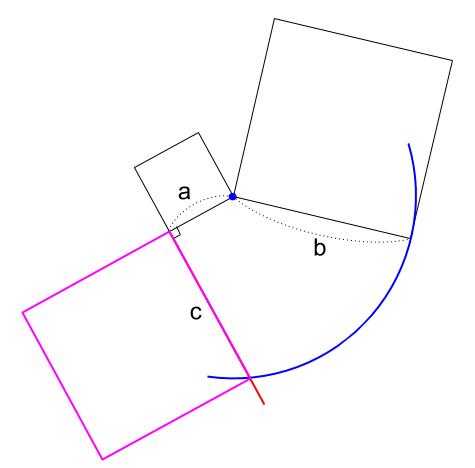
よって、水色の直角三角形をいかに作図するかを考えます。
等しい長さをとるのはコンパスの仕事ですから、
下図のように可能です。
赤い線は、はじめからある正方形の辺を延長します。
これで、直角がとれます。
青い円で、長さ \(b\) がとれます。
これで、長さ \(c\) がとれます。
ここから先は、どちら向きに正方形を作図してもかまいません。
正方形の作図がわからない人は、中学 \(1\) 年範囲ですので、
しっかりと基礎固めをしてください。
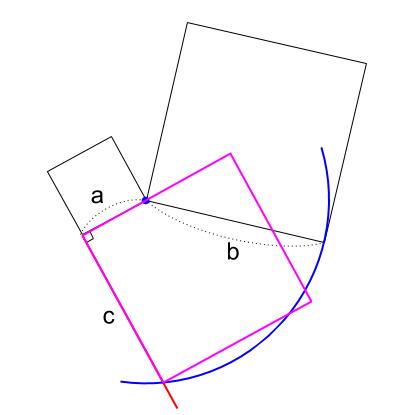
※もちろん、これ以外の箇所に作図する別解があります。
スポンサーリンク
