例題1
たてが \(12cm\),よこが \(18cm\) の長方形 \(ABCD\) で、点 \(P\) は点 \(B\) を出発して秒速 \(2\) cmで辺 \(AB\) 上を \(A\) まで動き、点 \(Q\) は点 \(P\) と同時に \(A\) を出発して、秒速 \(3cm\) で辺 \(AD\) 上を \(D\) まで動く。三角形 \(APQ\) の面積が \(24cm^2\) になるのは、点 \(P,Q\) が出発してから何秒後か求めなさい。
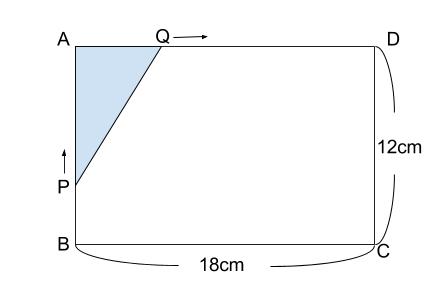
解説
\(x\) 秒後の図は以下のようになっている。
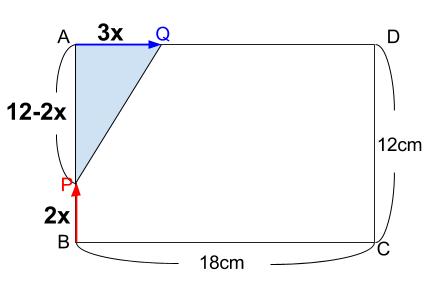
よって、以下のような模範解答例となる。
解答例
点 \(P,Q\) が出発してからの時間を \(x\) 秒とすると、三角形 \(APQ\) の面積 \(S\) は
\(S=\displaystyle \frac{3}{2}x(12-2x)\) となる。
\(S=24\) のときの \(x\) を求めます。
\(\displaystyle \frac{3}{2}x(12-2x)=24\)
\(x(6-x)=8\)
\(x^2-6x+8=0\)
\((x-2)(x-4)=0\)
\(x=2,4\)
\(x\) は \(0\) から \(6\) なので、
どちらも問題に適している。
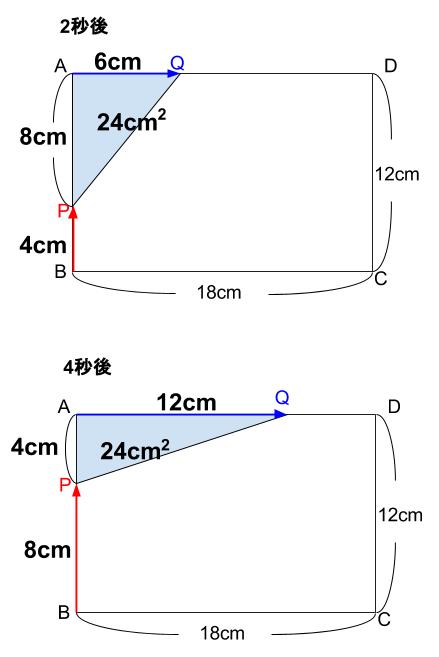
よって、\(2\) 秒後と \(4\) 秒後
例題2
たてが \(60cm\),よこが \(80cm\) の長方形 \(ABCD\) で、点 \(P\) は点 \(B\) を出発して秒速 \(3\) cmで辺 \(BA\) 上を \(A\) まで動き、点 \(Q\) は点 \(P\) と同時に \(D\) を出発して、秒速 \(4cm\) で辺 \(DA\) 上を \(A\) まで動く。三角形 \(APQ\) の面積が \(150cm^2\) になるのは、点 \(P,Q\) が出発してから何秒後か求めなさい。
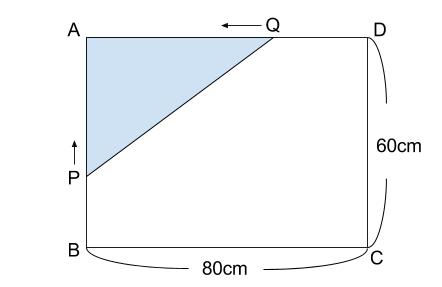
解説
\(x\) 秒後の図は以下のようになっている。
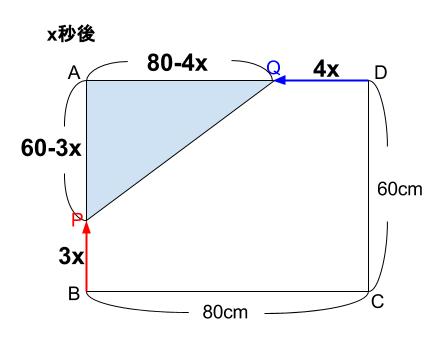
よって、以下のような模範解答例となる。
解答例
点 \(P,Q\) が出発してからの時間を \(x\) 秒とすると、三角形 \(APQ\) の面積 \(S\) は
\(S=\displaystyle \frac{1}{2}(60-3x)(80-4x)\) となる。
\(S=150\) のときの \(x\) を求めます。
\(\displaystyle \frac{1}{2}(60-3x)(80-4x)=150\)・・・①
\((60-3x)=3(20-x)\) , \((80-4x)=4(20-x)\) なので
①式は
\(\displaystyle \frac{1}{2}×3(20-3)×4(20-x)=150\)
\((20-x)^2=25\)
\(20-x=±\sqrt{25}\)
\(20-x=±5\)
\(-x=-20±5\)
\(x=20±5\)
\(x=15,25\)
\(x\) は \(0\) から \(20\) なので、
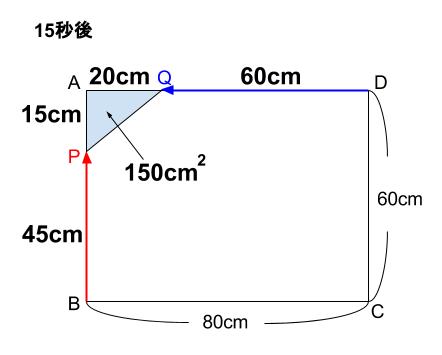
\(x=15\) のみ問題に適している。
よって、\(15\) 秒後
スポンサーリンク
