変化の割合って何だっけ?
\(1\) 次関数のときにもでてきた変化の割合です。
定義を覚えていますか?
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量}\)
です。
\(1\) 次関数 \(y=ax+b\) においては、
\(a=傾き=変化の割合\)
でした。
変化の割合は常に一定であり、ただの「\(a\)」 や「傾き」の別名でしかなかったものです。
\(2\) 乗に比例の \(y=ax^2\) においては、変化の割合は一定ではありません。
もちろん
「変化の割合= \(a\)」
という暗記もまったく無意味です。
ほとんどの場合、
変化の割合 ≠ \(a\)
です。
例題で確認をしましょう。
例題1
\(y=x^2\) において、\(x\) の値が \(1\) から \(3\) に増加するときの変化の割合を求めなさい。
解説
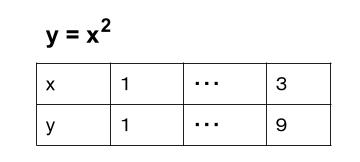
よって、
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量}= \displaystyle \frac{9-1}{3-1}= \displaystyle \frac{8}{2}=4\)
求める変化の割合は \(4\) です。
このように定義通り計算をすれば変化の割合を求めることはできます。
しかし・・
変化の割合とは結局何なのか・・・
これについて、その意味するところを下で説明してきます。
変化の割合というものの見方
そもそも変化の割合とは何なのでしょうか。
なぜそのようなものを定義したのでしょうか。
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量}\)
というものに注目することで、どんな利点があるのでしょうか。
ずばりお答えしますと
グラフの概形を知るため
なのです。
何のこっちゃわからん!という人。
落ち着いてください。
どんどん具体例でその意味を明らかにしていきますよ!
曲線のそっくりさんを、直線でかく
\(2\) 乗に比例の \(y=x^2\) のグラフをどのようにかいたか、覚えていますか?
\((0,0),(1,1),(2,4),(3,9),\)・・・
などの、グラフが通る点をいくつかとり、それを滑らかな曲線で結びました。
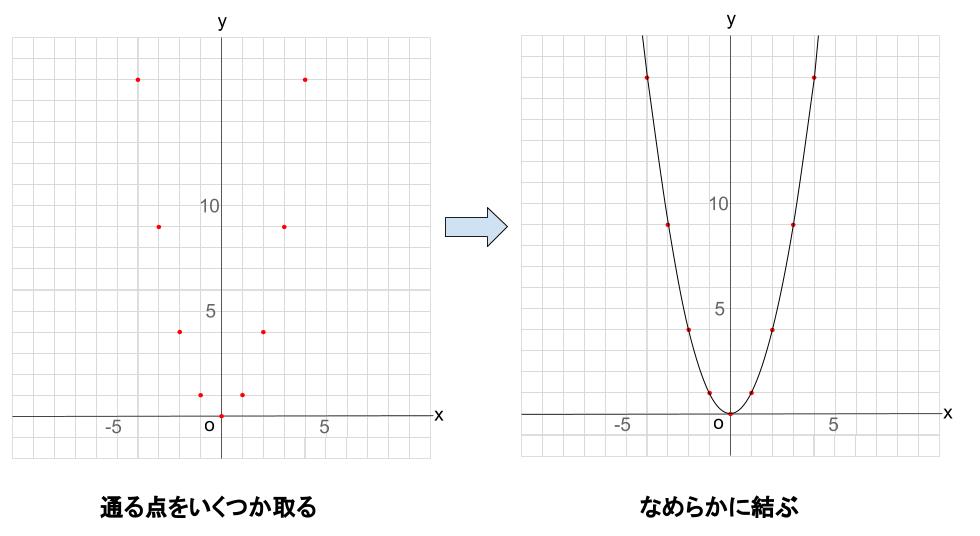
ところで・・・
「滑らかな曲線で結ぶ」という行為は、一体なにを根拠にやっているのでしょうか。
一体どういう意味の行為だったでしょうか。
覚えていますか?
ずばり
「無限個の点を取ることはできないから、完成図を知った上でなんとなくそれらしく見えるようにグラフをかいている」
という行為です。
つまり、「完璧に正確なグラフはかけないなら、ある程度似ていればいいだろう」
という行為です。
直線で、\(y=x^2\) のグラフを近似
実際、\(2\) 乗に比例の \(y=x^2\) のグラフのそっくりさんを、直線で書いてみましょう。
\(y=x^2\) が通る点、\((0,0),(1,1),(2,4),(3,9),\)・・・を直線で結びます。
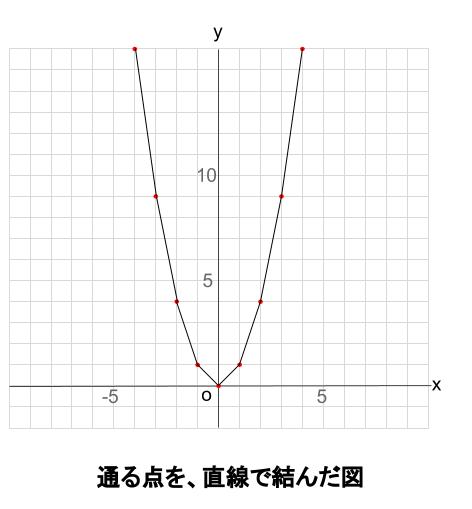
どうですか。
\(y=x^2\) のグラフに似ていますか?
結構似てますよね!?
似ていない・・・って言いたい人の声が聞こえてくるようです。
では、(\(\displaystyle \frac{1}{2}\) ,\(\displaystyle \frac{1}{4})\) もいれてみましょう。
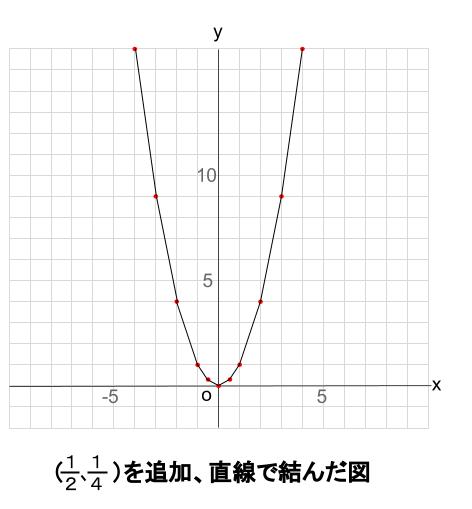
どうでしょう。ずいぶんと知っているグラフの形に近づきましたね。
もっともっと通る点を増やしていけば、
どんどん本当の曲線に近づけていくことができるわけです。
しかし!!
結局は無限の点をとることができない以上、どこかで諦めるしかありません。
曲線の究極の姿は分からないが、その一部分がどのような概形なのか、おおよその姿を直線を用いて知る。
これこそが「変化の割合」という概念なのです。
曲線を、直線で近似するということです。
もう一度上で解いた例題を解説します。
例題1(再掲)
\(y=x^2\) において、\(x\) の値が \(1\) から \(3\) に増加するときの変化の割合を求めなさい。
解説
\(y=x^2\) において、
\(x=1\) のとき \(y=1\)
\(x=3\) のとき \(y=9\)
これを図示すると、
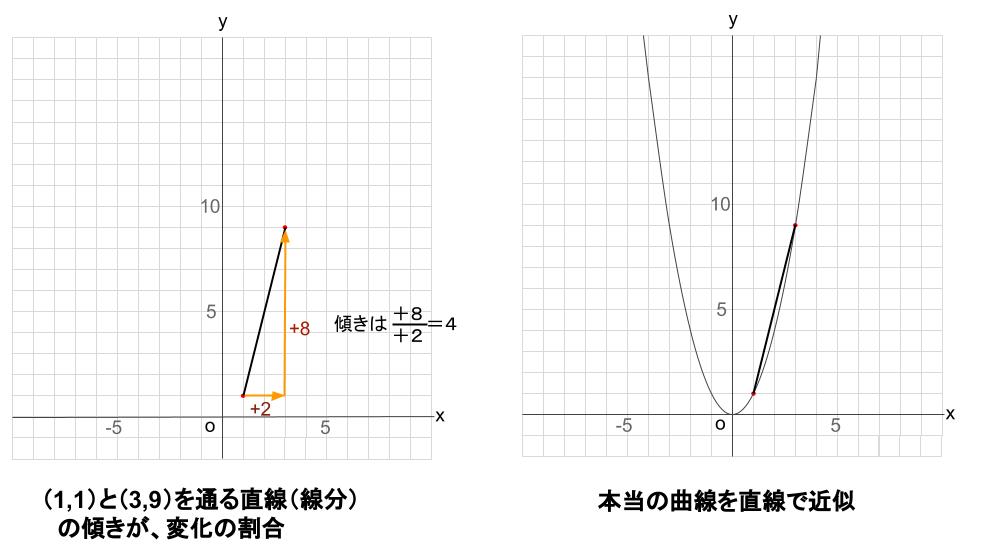
変化の割合とは、曲線の一部分を直線と見立てたとき、その傾きはいくらか
という意味です。
\(x\) の値が \(1\) から \(3\) に増加するときの変化の割合(直線の傾き)は、
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量} = \displaystyle \frac{8}{2}=4\)
と求まります。
例題2
\(y=-x^2\) において、\(x\) の値が \(-2\) から \(1\) に増加するときの変化の割合を求めなさい。
解説
上で説明したとおり、変化の割合とは曲線を直線でまねっこすることです。
しかし・・・
この例題2は、そのような基礎概念を無視したとんでもない問題なのです。
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量} \)
に当てはめて計算して、
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量} =\displaystyle \frac{+3}{+3} =1\)
と求めることはできます。
実際にこの例題2の答えは \(1\) です。
しかし、この問題の意味するところは下図のようになります。
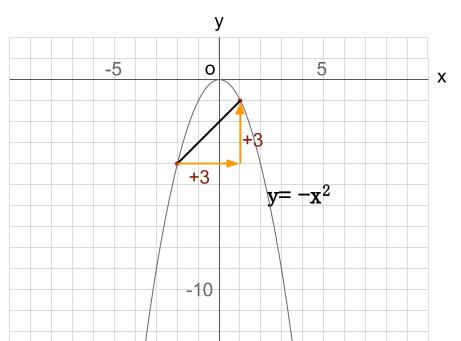
曲線を直線でまねっこしようという思想が完璧に無視されています。
\(y=ax^2\) において、原点をまたいだ変化の割合を考えることなどほぼ無意味です。
しかし、
\(変化の割合 = \displaystyle \frac{yの増加量}{xの増加量} \)
という式に当てはめて計算させることだけを目的としたこのタイプの問題も
中学校の定期試験ではよく出題されているようです。
このタイプの問題に出会ったら、ぜんぜん曲線を近似できてないけどね!
と割り切って、無意味な直線の傾きを計算しましょう。
スポンサーリンク
