例題1
下の図のように、正方形の紙と長方形の紙がある。長方形の横の長さは、正方形の \(1\) 辺より \(2cm\) 短く、たては \(10cm\) 長い。また、この長方形の紙の面積は正方形の紙の面積の \(1.5\) 倍より\(6cm^2\) 小さい。このとき、正方形の \(1\) 辺の長さを求めなさい。
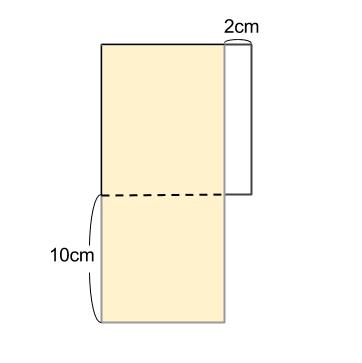
解説
問題文でかかれていることを等式にすることが第一目標ですね。
\(正方形の面積×1.5-6=長方形の面積\)
となります。
これを指針に解答を書いていきます。
解答
正方形の \(1\) 辺の長さを \(xcm\) とする。
正方形と長方形の面積について、下のようの式になります。
\(x^2 ×1.5 -6 =(x-2)(x+10)\)
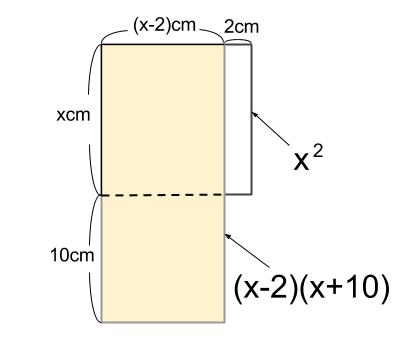
ここから先は方程式を解くのみです。
\begin{eqnarray}x^2 ×1.5 -6 &=& (x-2)(x+10) \\x^2 ×1.5 -6 &=& x^2+8x-20 \\0.5x^2-8x+14 &=& 0 \\x^2-16x+28 &=& 0 \\(x-2)(x-14) &=& 0\end{eqnarray}
\(x=2\) または \(x=14\) なので
\(x=2,14\)
方程式が解けましたが、これをあわてて答えとしてはいけません。
題意に適するのかどうかを調べるのです!!
正方形の \(1\) 辺が \(2cm\) だったら・・・
よこの長さが \(2cm\) 短い長方形をつくることはできません。
よって、これはこの文章題の答えには適しません。
正方形の \(1\) 辺が \(14cm\) だったら・・・
可能ですね。
問題の通りです。
より、答えは \(14cm\) です。
2次方程式の解は、文章題に適するのか?
たいていの \(2\) 次方程式は、解を \(2\) つ持っています。
※例外もあり、解が \(1\) つだけの \(2\) 次方程式もありましたね。
このとき、出てきた解が、文章題の答えとして適しているかどうかを調べることが必須です。
上の例題のように、\(x=2\) は、この問題の答えとして明らかにおかしい。
このような解がでてくることがあるのが、\(2\) 次方程式なのです。
どうしてそんなことが起こるのか、なんだか不思議な気持ちになっている人もいるかもしれませんね。
なぜなのかについて簡単にいうと、「文章題と \(2\) 次方程式が、完全に同じものではない」からです。
文章題の仕組みが、\(2\) 次方程式の一部と一致しているのです。
なんだかぜんぜんわからない!!って声が聞こえてきそうです。
とりあえず、\(2\) 次方程式ではこのようなことが起こるのだ!としっかり覚えておいて下さい。
それで何の問題もありません。
文章題においては、\(2\) 次方程式の解が、題意に適するかどうか、確かめをする!
確実に覚えて、そして実行してくださいね!!
例題2
ある数から \(4\) を引いて \(2\) 乗した値は、ある数の \(8\) 倍から \(12\) を引いた値と等しい。
ある数を求めなさい。
解答
ある数を \(x\) とすると
\((x-4)^2 = 8x-12\)
あとはこの \(2\) 次方程式を解くだけです。
\begin{eqnarray}x^2-8x+16 &=& 8x-12 \\x^2-16x+28 &=& 0 \\(x-2)(x-14) &=& 0\end{eqnarray}
\(x=2,14\)
解けました。
これを急いで答えとするのではなく、問題に適しているかどうかを調べます。
これは、どちらも問題に適しています。
\(x=2,14\)・・・これはどちらもOK!
よって、求める数は、\(2,14\)
異なる文章題から、同じ2次方程式がでてきた!
さて、すでに気づいている人も多いかもしれませんが、
例題1と例題2、まったく異なる問題でしたが、
その文章の通り方程式をたてると、どちらも
\(x^2-16x+28=0\)
という、同じ \(2\) 次方程式となりました。
先ほど、 「文章題と \(2\) 次方程式は完全に同じではない」と書きました。
なんとなくその雰囲気をわかってもらえたでしょうか?
スポンサーリンク
