変域のあるグラフ
例題1
次の関数について、 \(y\) の変域を求めなさい。
\(y=3x^2\)
\(-2 \leqq x \leqq1\)
解説
大雑把にグラフをかくことを強くお勧めします。
\(y=ax^2\) のグラフの概形(おおまかな形、特徴)は覚えていますね!?
下図のような原点を通る曲線(放物線)になります。
薄くかくのがコツです。
どの点を通るかなど、細かいことは一切無視してかきます。
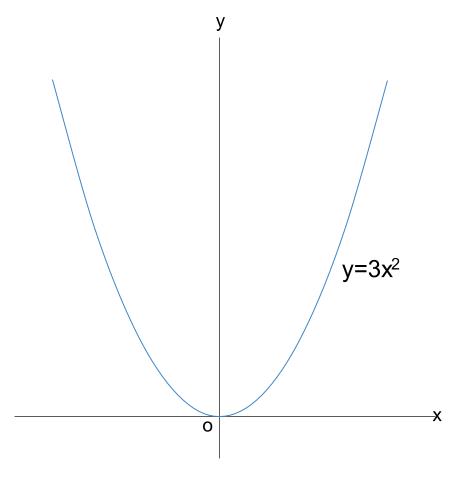
変域の端である、\(x=-2\) から \(x=1\) までを図示しましょう。
先ほど薄くかいたものを、濃くなぞればOKです。
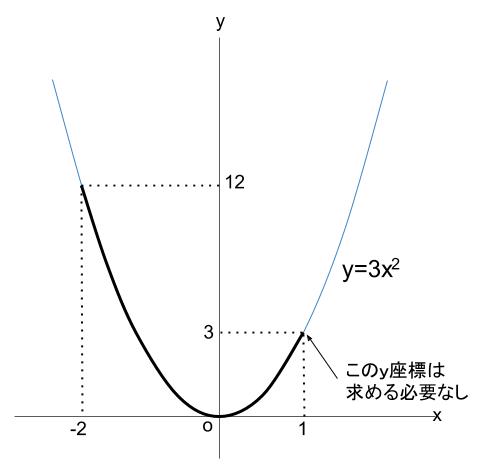
図をみれば明らかです。
\(y\) の変域は \(0 \leqq y \leqq12\) です。
例題2
関数 \(y=ax^2\) で、\(x\) の変域が \(-4 \leqq x \leqq2\) のとき
\(y\) の変域が \(-8 \leqq y \leqq0\) である。\(a\) の値を求めなさい。
解説
必ずグラフの概形をかいて考えます。
数学は、目で見て解くのが最大のコツです。
無理に暗算(計算だけでなく、図もかかないこと)する必要はありません。
\(y\) の変域が \(-8 \leqq y \leqq0\) なので、
これは比例定数が負の場合とわかります。
グラフの概形は以下のようになります。
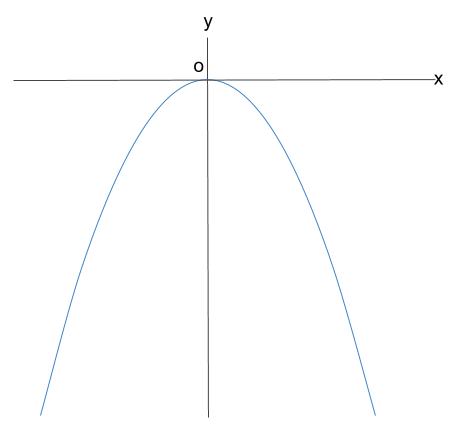
\(x\) の変域が\(-4 \leqq x \leqq2\) なので、
変域の端である、\(x=-4\) から \(x=2\) までを図示しましょう。
\(y\) の変域が \(-8 \leqq y \leqq0\) なので、
\(x=-4\) のときに \(y=-8\) であることがわかります。
図からわかるのですよ!
図をかくことが大切なのですね。
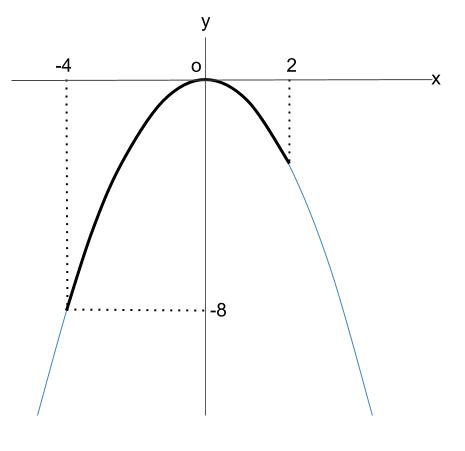
よって、\(x=-4\) とき、\(y=-8\) なので
\(x=-4\)、\(y=-8\) を \(y=ax^2\) に代入して
\(-8=a×(-4)^2\)
\(-8=16a\)
\(a=-\displaystyle \frac{1}{2}\)
より、求める放物線の式は
\(y=-\displaystyle \frac{1}{2}x^2\)
です。
スポンサーリンク
