グラフの読み取り
\(2\) 乗に比例(\(2\) 次関数)のグラフを読みとることも、非常に重要です。
例題1
下の図の放物線の式を求めなさい。
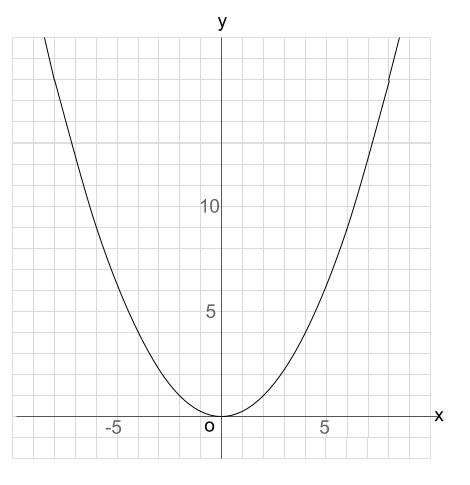
解答
原点を通る放物線なので、
放物線の式は
\(y=ax^2\)
となります。
※もちろん \(y=ax^2\) しか出題されない、という暗記でもかまいません。
中学生の範囲では、それしか出題されないからです。
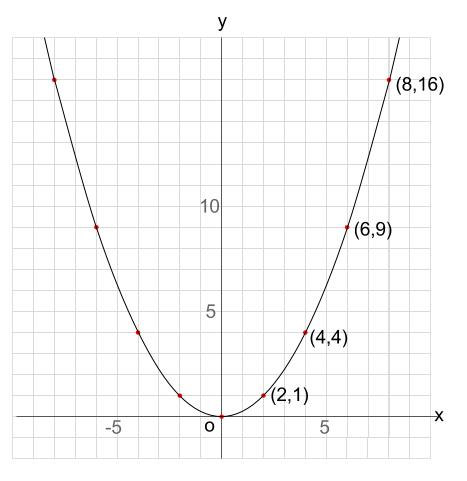
あとは、グラフ上の点で、\(x\)、\(y\) 座標がともに整数の点(格子点)を探し、
それを式に代入します。
\((2,1)\) がみつかるので、 \(y=ax^2\) に代入します。
他にも \((4,4)\) や \((6,9)\) や \((8,16)\) があり、そのどれを代入してもOKです。
\(1=a×2^2\)
\(a=\displaystyle \frac{1}{4}\)
よって求める放物線の式は、
\(y=\displaystyle \frac{1}{4}x^2\)
例題2
下の図の放物線の式を求めなさい。
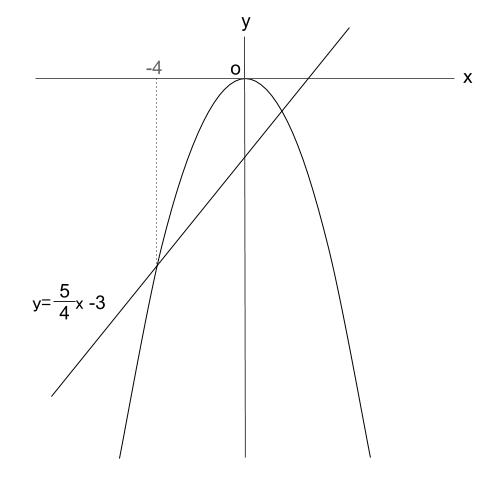
解答
直線の式が与えられているので、これを利用します。
直線と放物線の交点を \(A\) とすると
\(A\) は直線上の点で \(x\) 座標が \(-4\) なので、これを直線の式 \(y=\displaystyle \frac{5}{4}x-3\) に代入して
\(y=\displaystyle \frac{5}{4}×(-4)-3\)
\(y=-8\)
より、点 \(A\) の座標は \((-4,-8)\)
この点 \(A\) は、放物線上の点なので、
\(y=ax^2\) に \(x=-4\) \(y=-8\)
を代入して
\(-8=a×(-4)^2\)
\(-8=16a\)
\(a=-\displaystyle \frac{1}{2}\)
よって、求める放物線の式は
\(y=-\displaystyle \frac{1}{2}x^2\)
スポンサーリンク
