【中学数学】相似な図形の体積比

相似な図形の体積比

相似な図形の体積比は相似比の $3$ 乗の比になります。

つまり、相似比 $a:b$ の空間図形の体積の比は $a^3:b^3$ です。

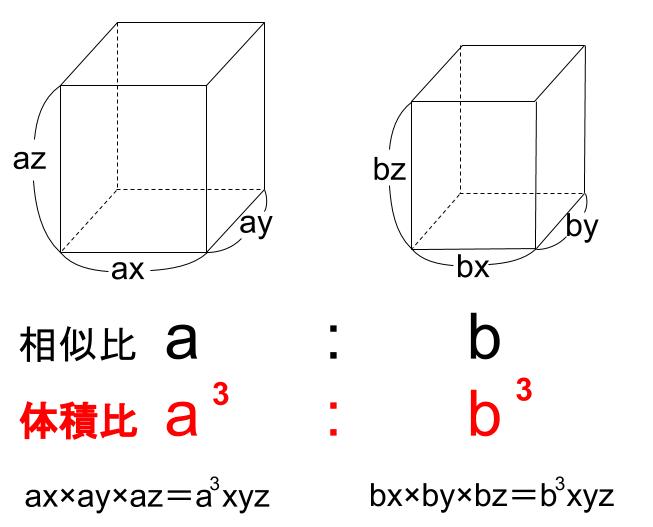
たての比も $a:b$
よこの比も $a:b$
高さの比も $a:b$ なので
体積の比は $a×a×a:b×b×b$ となるわけです。

もちろん、直方体だけでなく、
あらゆる空間図形で相似な図形ならば、
体積比は相似比の $3$ 乗の比が成り立ちます。

例題１

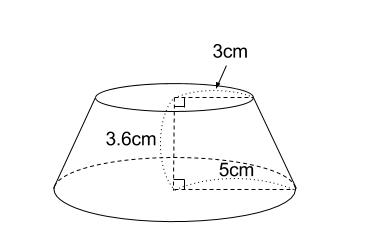
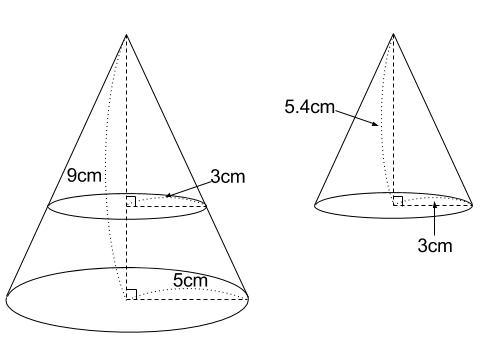
下の図の円すい台の体積を求めなさい。

解説

円すい台は、円すいから円すいを切りとった立体です。

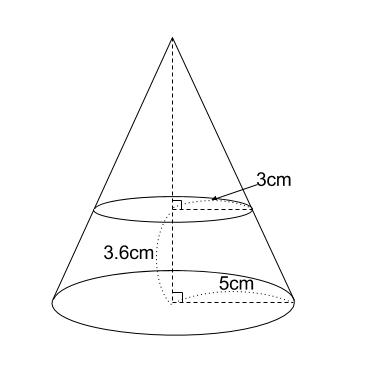
つまり、底面の半径 $5cm$ の円すいから
底面の半径 $3cm$ の円すいを切り取ってできた円すい台の体積を
求めます。

底面の半径 $5cm$ の円すいの高さを求めるために
下図の水色の三角形に着目します。

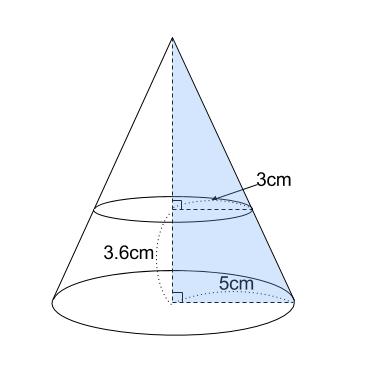
ピラミッド型の相似で、相似比が $5:3$ なので、
高さの比も $5:3$ です。

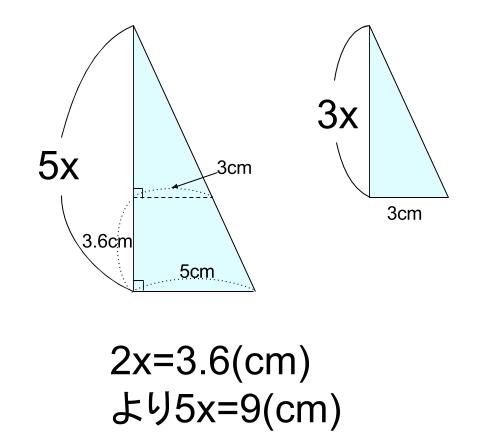
$2x=3.6(cm)$ なので、
$5x=9(cm)$
です。

つまり、 $2$ つの円すい台は下のようになっています。

大円すいの体積を求めて、
小円すいの体積を求めて、
その差を出せば、それが求める円すい台の体積です。
この方法で答えを求めてもかまいませんが、
$2$ つの円すいが相似なので、
相似な立体の体積比を用いて円すい台の体積を求めましょう。

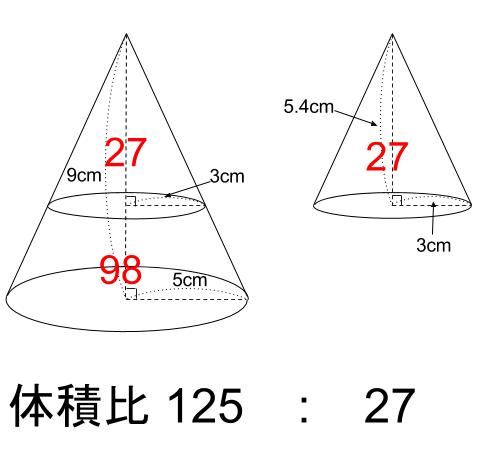
相似比が $5:3$ の立体の体積比は $5^3:3^3=125:27$
なので、大きい円すいと、円すい台の体積比は $125:125-27=125:98$
となります。

よって、円すい台の体積は、大きい円すいの体積の $\displaystyle \frac{98}{125}$ で求まります。
$5^2 \pi ×\displaystyle \frac{1}{3}×9×\displaystyle \frac{98}{125}=\displaystyle \frac{294}{5}\pi$

と求まります。

答えの値が求まってうれしいのですが、
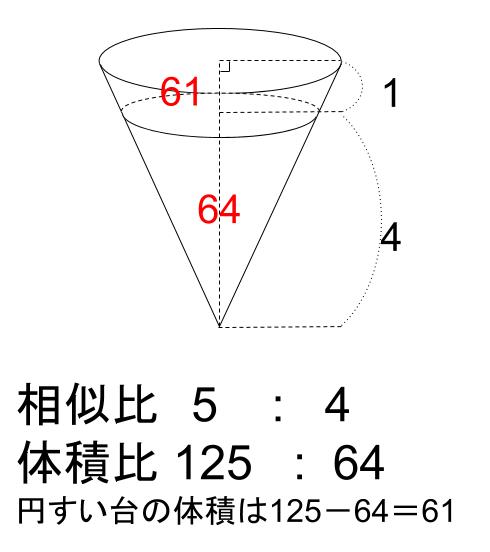
そんなことより、小さい円すいと円すい台の体積が $4$ 倍近く違うって驚きませんか？

ちなみに、

ソフトクリームのコーン部分を、ほぼ半分に分けるには、
相似比 $5:4$ で分けないといけないんです。
この結果は、ちょっとびっくりしませんか？
悪用もできそうですね・・・

※コーン(cone)とは英語で円すいのことです。

• 次のページ 直角三角形の相似
• 前のページ 相似な図形の面積比